This is the second part of the explorative series on Perlin Noise in P5JS and Processing, and focuses on applying Perlin Noise to a 2 dimensional grid of items on the canvas and how we can obtain interesting surfaces and textures in this manner.
We've already had a look at scrolling perlin noise across the canvas by increasing one or multiple noise parameters over time. However, creativity doesn't stop there!
Quantizing the noise values
I'm not sure if this specific technique has a name, but it essentially consists of quantizing the value from the nosie() function. When we feed grid coordinates (scaled by some scale parameter), the noise() function returns smooth and continuous values that resemble a landscape. We can use this to create interesting patterns in combination with quantization. Think about it like a real lanscape, where we shave off mountain tops that are higher that a very specific altitude, and flatten everything around it. The formal definition of quantization is:
Quantization is the process of constraining an input from a continuous or otherwise large set of values (such as the real numbers) to a discrete set (such as the integers).
A simple cisual example in code:
function setup() {
createCanvas(301, 301);
t = rez = c = n = 0.008;
strokeWeight(3);
}
function draw() {
background(0);
noStroke();
for (i = 0; i < height; i += 3) {
for (j = 0; j < width; j += 3) {
n = noise(i * rez, j * rez);
//uncomment the next line to see difference between noise() and random()
//n = random()
if(n>0.6){
fill(255);
}else{
fill(0);
}
rect(i, j, 3);
}
}
noLoop()
}
This allows us to obtain these blob like separation between the black and white areas:


If we were to replace the noise() function with random, we would get something that is much more similar to static noise:


Obviously, we are not limited to quantizing to only two distinct values, we could quantize to an arbitrary amount of values. Here I'm using ternary conditional statements:
function setup() {
createCanvas(301, 301);
t = rez = c = n = 0.008;
strokeWeight(3);
}
function draw() {
background(0);
noStroke();
for (i = 0; i < height; i += 3) {
for (j = 0; j < width; j += 3) {
n = noise(i * rez, j * rez + t) * 3;
n > 3
? (c = 3)
: n > 2
? (c = 2)
: n > 1
? (c = 1)
: (c = 0);
fill(c*100);
rect(i, j, 3);
}
}
t += 0.01;
}

Landscape
In this manner we could quantize the values to different colors and obtain and almost landscape like scrolling surface:
function setup() {
createCanvas(400, 200);
t = rez = c = n = 0.005;
strokeWeight(3);
cols = [
"#f94144",
"#f3722c",
"#f8961e",
"#f9844a",
"#f9c74f",
"#90be6d",
"#43aa8b",
"#4d908e",
"#577590",
"#277da1",
];
}
function draw() {
background(0);
noStroke();
for (i = 0; i < width; i += 3) {
for (j = 0; j < height; j += 3) {
n = noise(i * rez, j * rez + t) * 10;
n > 9
? (c = 9)
: n > 8
? (c = 8)
: n > 7
? (c = 7)
: n > 6
? (c = 6)
: n > 5
? (c = 5)
: n > 4
? (c = 4)
: n > 3
? (c = 3)
: n > 2
? (c = 2)
: n > 1
? (c = 1)
: (c = 0);
fill(cols[c]);
rect(i, j, 3);
}
}
t += 0.01;
}

Landscape + Tiling
function setup() {
createCanvas(301, 301);
t = rez = c = n = 0.02;
strokeWeight(3);
}
function draw() {
background(0);
noStroke();
for (i = 0; i < height; i += 3) {
for (j = 0; j < width; j += 3) {
n = noise(i * rez, j * rez + t);
if(n > 0.5){
fill(0);
}else{
fill(127.5*127.5*sin(i*0.02+millis()/1000),
127.5*127.5*cos(j*0.02+millis()/1000),
127.5)
}
rect(i, j, 3);
}
}
t += 0.08;
}

if(n > 0.5){
fill(127.5*127.5*sin(i*0.02+millis()/3000),
127.5,
127.5*127.5*cos(j*0.02+millis()/3000),)
}else{
fill(127.5*127.5*sin(i*0.02+millis()/3000),
127.5*127.5*cos(j*0.02+millis()/3000),
127.5)
}

Truchet Tiling
We can also mess around with simple truchet tiling, where the angle of the line is determined by the value of the noise at that particular point:
function setup() {
createCanvas(301, 301);
t = rez = c = n = 0.02;
strokeWeight(2);
}
function draw() {
background(0);
//noStroke();
stroke(255)
for (i = 0; i < height; i += 10) {
for (j = 0; j < width; j += 10) {
n = noise(i * rez, j * rez + t);
if(n > 0.5){
line(i,j,i+10,j+10)
}else{
line(i+10,j,i,j+10)
}
}
}
t += 0.01;
}

We can get more creative with this by offsetting the tiles differently:
if(n > 0.5){
line(i+n*10,j+n*10,i+10,j+10)
}else{
line(i+10,j,i,j+10)
}

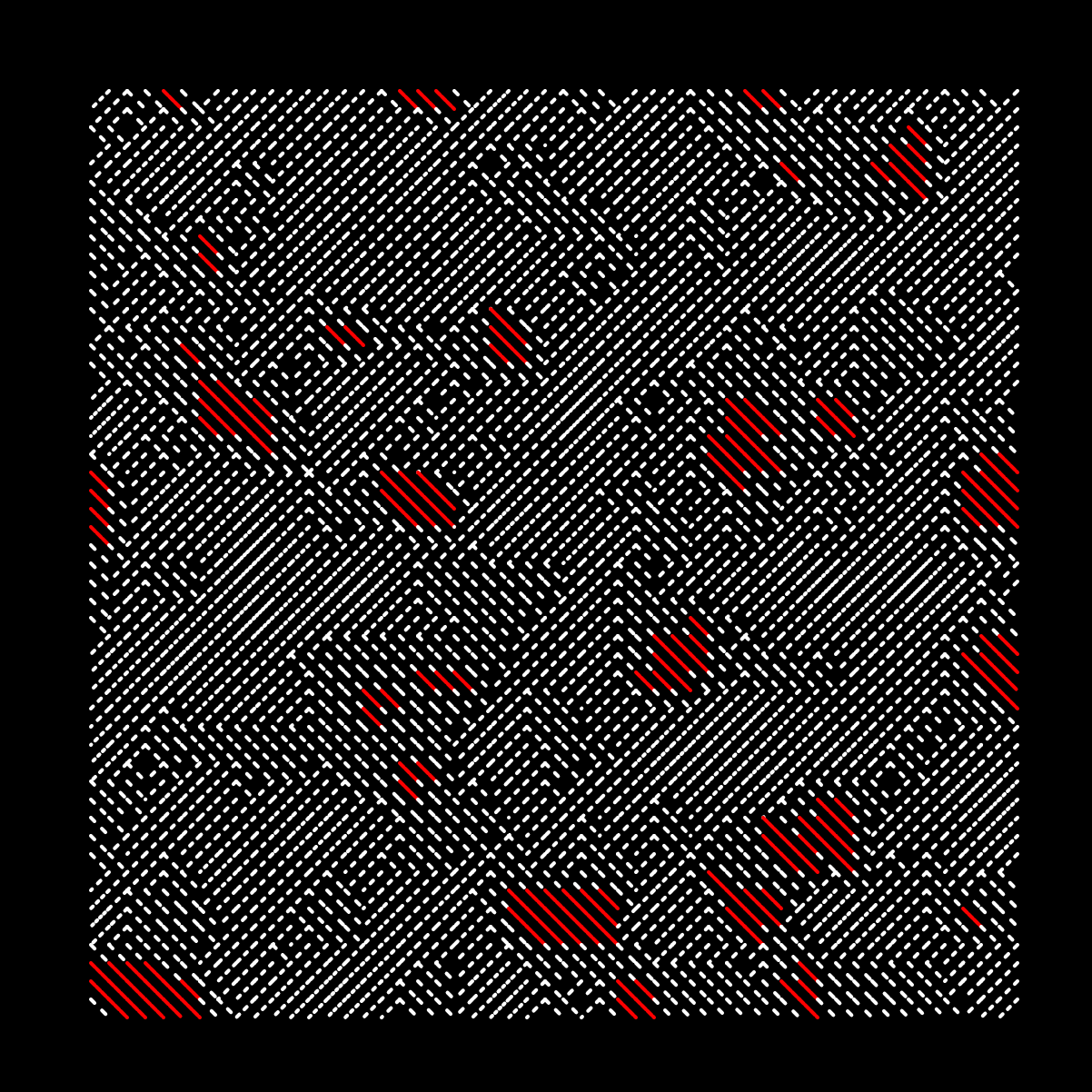
Equivalently we can add more conditional statements to make this texture more interesting, and don't necessarily have to animate it:
function setup() {
createCanvas(601, 601);
t = rez = c = n = 0.022;
strokeWeight(2);
frameRate(30)
//createLoop({duration:5, gif:true})
xOff = 50
yOff = 50
}
function draw() {
background(0);
//noStroke();
stroke(255)
for (i = xOff; i < width-xOff; i += 10) {
for (j = yOff; j < height-yOff; j += 10) {
n = noise(i * rez, j * rez + t);
drawingContext.setLineDash([n*5,n*10])
if(i - 40 < mouseX && i + 40 > mouseX
&& j - 40 < mouseY && j + 40 > mouseY){
drawingContext.setLineDash([n*5,n*10])
}
if(n>0.65){
drawingContext.setLineDash([n*5,1])
stroke(255,0,0)
}else{
stroke(255)
}
if(n > 0.5){
line(i,j,i+10,j+10)
}else{
line(i+10,j,i,j+10)
}
}
}
t += 0.01;
noLoop();
}
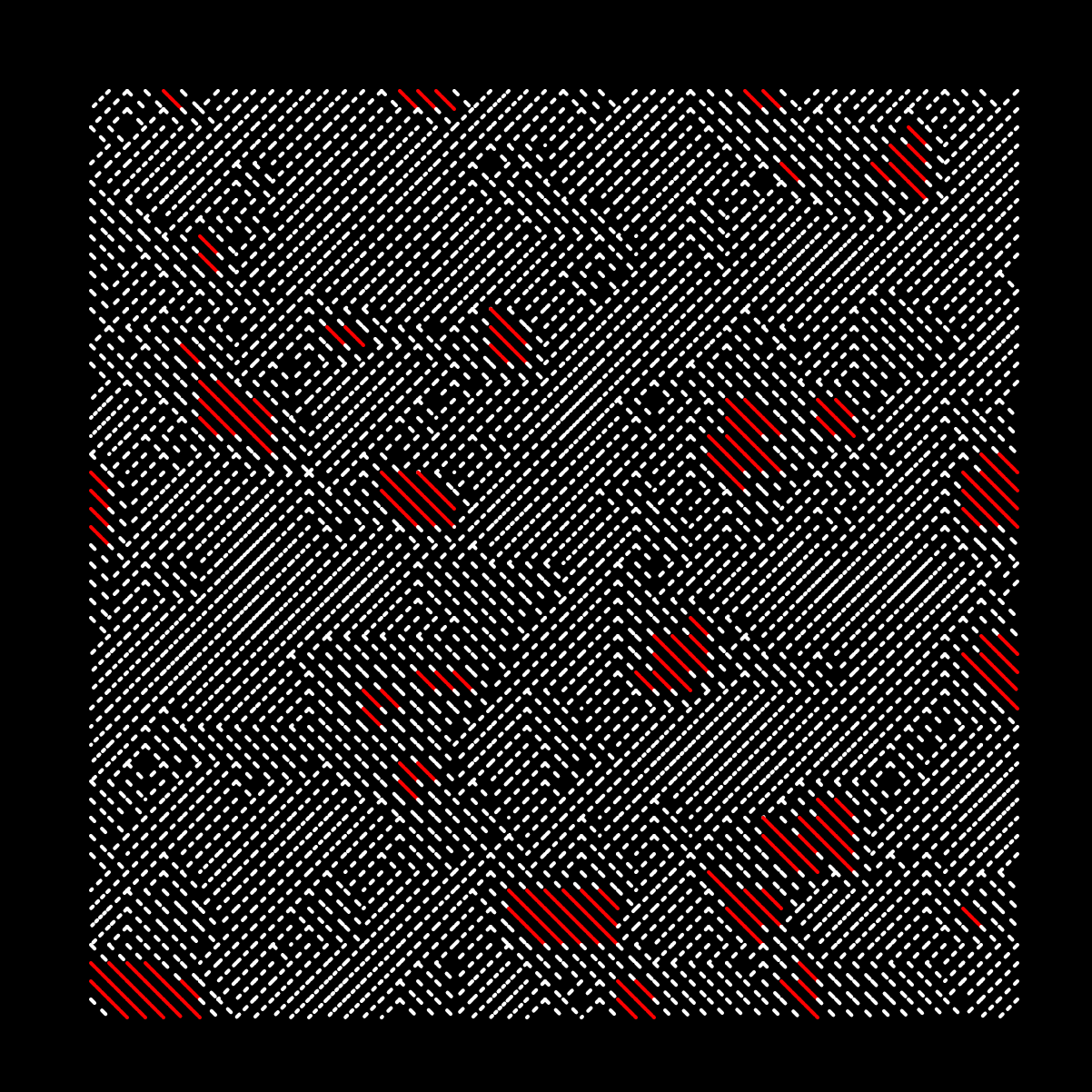
Alternatively we can also animate this and add more variation:
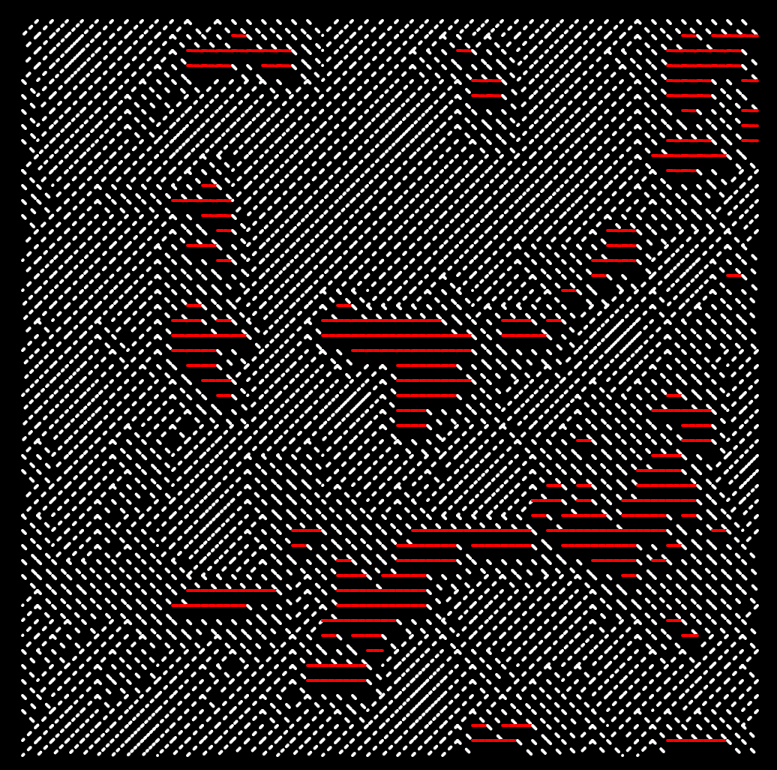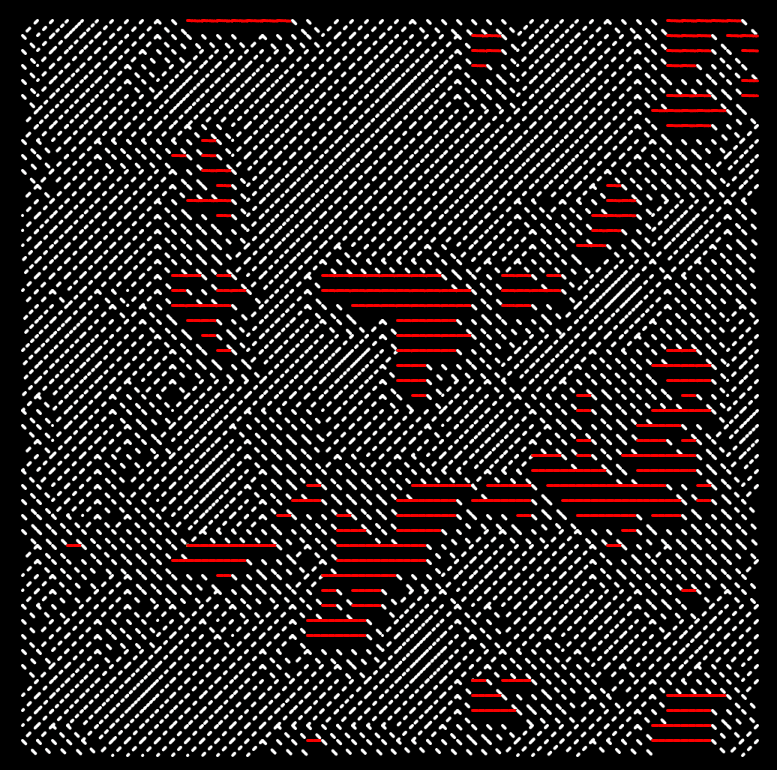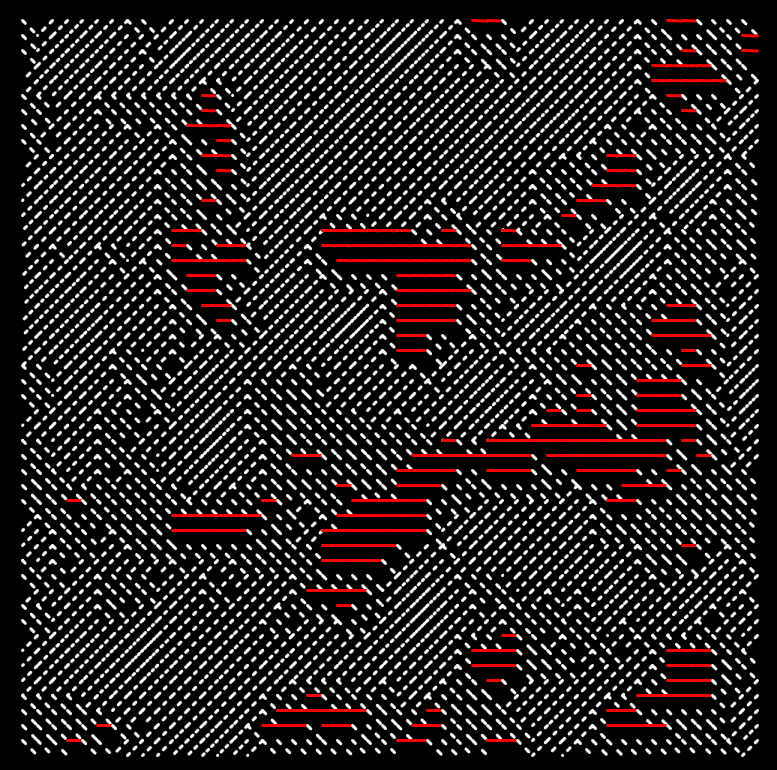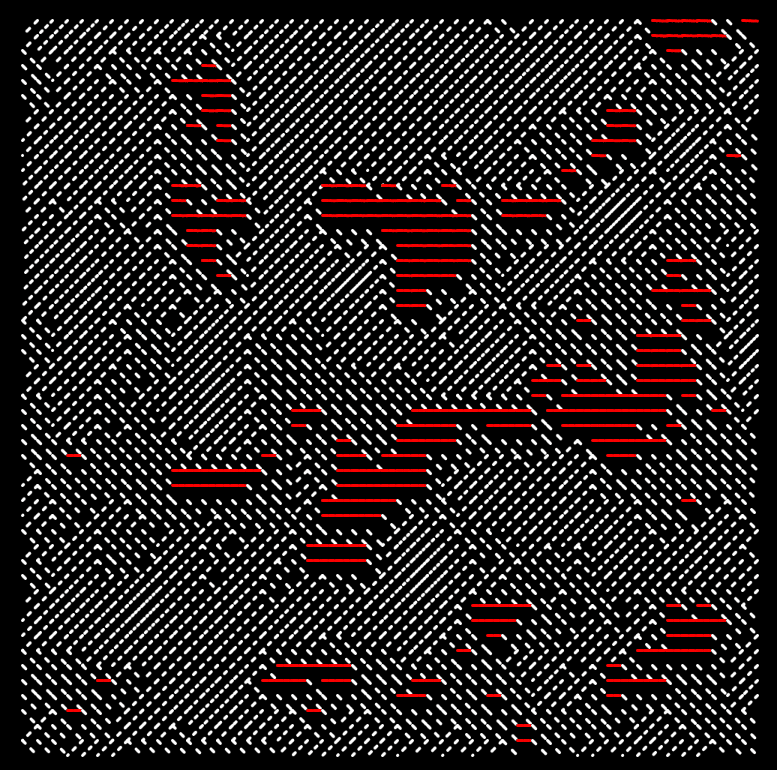
And that's is it for this article! If you've enjoyed this post consider sharing it on your socials, with friends and/or family that share an interest in creative coding - otherwise cheers and happy sketching ~ Gorilla Sun 🌸