This blog post is about the age-old creative coding problem of shape packing! Even though it might seem like a simple task at first, it is actually quite an involved undertaking. It also usually entails having a broader look at how collision detection algorithms work. In the following sections we'll work our way up to an algorithm with which you can essentially pack any sort of geometric shapes, and combinations thereof.


Before we begin, I want to point out that I had a first encounter with this algo back in February of 2022. I never completed that particular idea, but it led to an interesting packing scheme. You can see some of the artworks my code produced above.
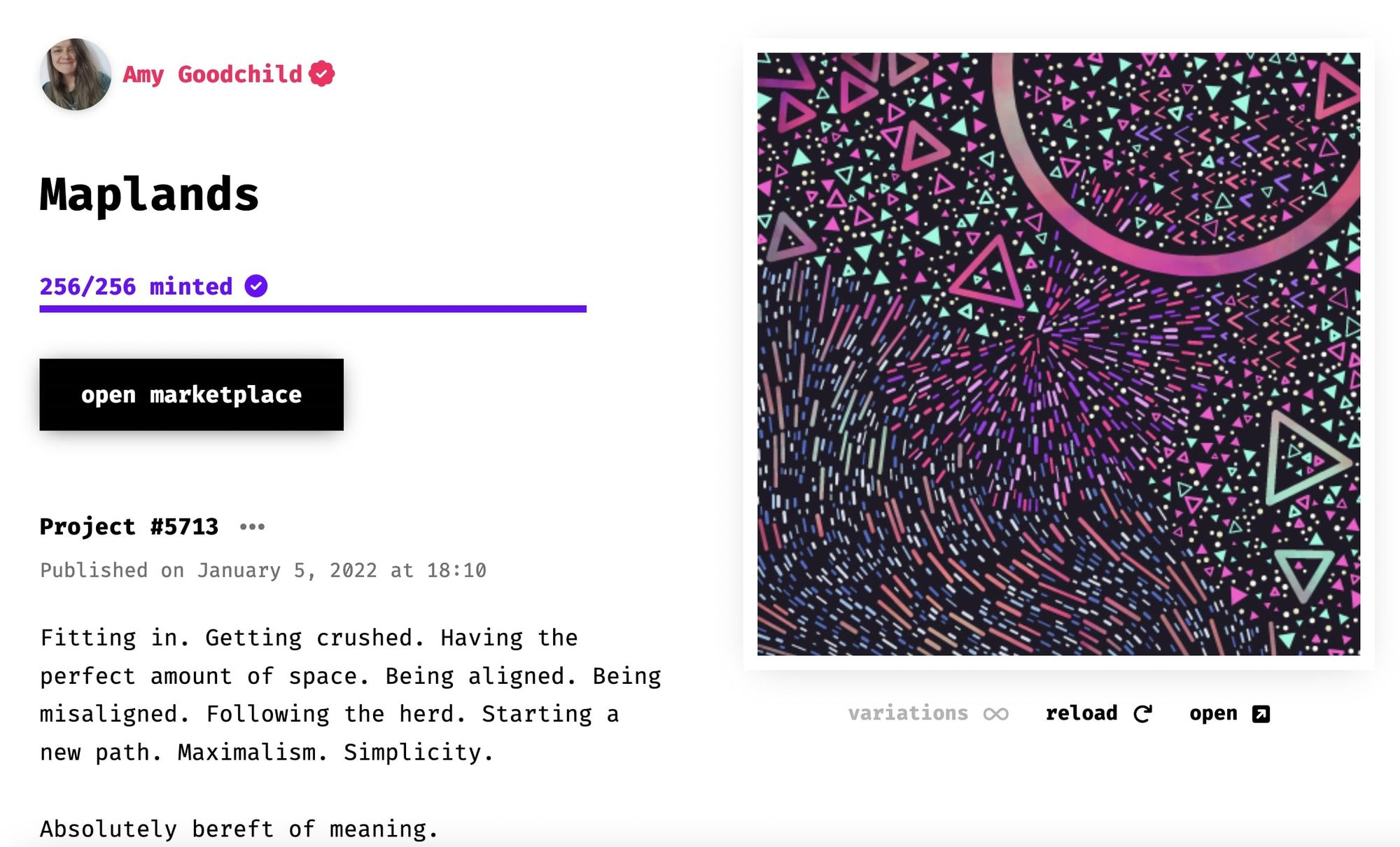
I also recently learned that a few others have made their own version of this idea. In June I faced a packing problem where I had to draw all sorts of geometric shapes to the canvas. I was left scratching my head at first and it took me quite a while to find a solution. While researching different methods I came across Amy Goodchild’s writeup on a wonderful sketch of hers called "Maplands" where she used a similar strategy to what I ultimately did to implement my idea.

Later on I also re-discovered Tarwin Stroh-Spijer's fruit salad packing sketch, which initially evolved from Jeff's (aka ippsketch) banana packing sketch. I had a thorough look at Tarwin's beautifully written packing library, and a lot of the code in later sections of this post are based on Tarwin's method. Go check out the folks mentioned above, they're all awesome creative individuals!
Discussion:
- Packing Algorithms in Generative Art
- Strategies for Collision Detection
- Collision Detection in Video Games
- Proposed Solution
Getting our hands dirty:
- A closer look at Tarwin's Circle Packing Library
- Generalizing for other Shapes
- Compositing Shapes with Circles
- The Shape Packing Procedure
- Complete Example
- Closing Notes
Packing Algorithms in Generative Art

Packing problems come in various flavours, but generally their overarching concern is positioning items as densely as possible within a given area. Despite its deceptive simplicity, bin packing is actually an NP-Hard problem, with it's associated decision problem (checking if the items to be packed fit in a certain area), is NP-Complete. Understanding this is not necessary for what follows however. I just find it incredibly interesting though, I keep finding myself coming back to this problem thinking: "Surely this can't be this difficult!"
Packing algorithms are useful for a range of real life scenarios, such as packing boxes in a warehouse, or positioning shapes on a sheet of laser cutting material such that the amount of wasted material is minimised. Packing is a heavily researched area of mathematics and fairly advanced algorithms have been developed to solve different variations of it. In generative art the primary goal of packing algorithms is often the creation of visually pleasing and interesting packing patterns. We also often don't start with shapes that have a pre-determined size (usually real life objects have a pre-determined size duh), but make them up on the go.
Hence gen-art packing algorithms vary a little in that regard. I'd like to show off a few artworks that have in one another or another been made with packing algorithms. Here's two stunning artworks from Caleb Ogg:


Caleb's pieces Lens 3 and Colorshift 2, part of his ongoing 'Coalesce' series, are some of the most interesting circle packing sketches I've seen in a while. Note that the images shown here (2000x2000px) don't do the originals justice which are absolutely gigantic (16000x16000px). Built on a system of circles and rings, Caleb makes use of an underlying noise field for a nifty creative effect. I especially like how Lens conveys the illusion of multiple overlapping lenses that appear to contort the coloration of the underlying circles, which is done by scaling and multiplying the underlying noise field. Excited to see where this series is heading, always a pleasure when Caleb's sketches bless my timeline.
A little less recent example of a circle packing sketch is by none other than Jared Tarbell:

As well as this beautiful homage to Jared's sketch by prolific creative coder Dmitri Cherniak:

If you like these patterns you should also check out the Appolonian Gasket (alternatively Appolonian circle packing). And for good measure we also need to mention Yann LeGalle who just utterly blows my mind on a regular basis:
And one of the earliest ones that captivated me and initially motivated me to explore circle packing for myself was this sketch by Piter Pasma's:
I really love this one. The squares are positioned in such a way that circles emerge in a wiggly centered wiggly line, as if an invisible force was repelling them. And indeed that invisible force is most likely an additional constraint that doesn't allow rectangles to be placed if the interesect with the phantom circles. I also really love the hachure lines that get more pronounced the close they get to the circles. All in all a really beautiful composition. And for the plotter lovers we need to also mention plotter afficionado Gaëtan Renaudeau (aka Greweb) who's made some really gorgeous plots in that regard:
In the next section we'll have a closer look at collision detection. We usually require a way to check for collisions between the shapes that we are packing, to see if we inserted a shape at a valid location and that it isn't intersecting or overlapping with other shapes. In this blog post we'll only consider static examples where things don't move around once they've been placed on the canvas. Collision detection however generally is a topic accompanied by moving things, as it is often the case in video games. Think of a classic game like Space Cadet Pinball, or, to give another example, top down 2D billiard simulations. What goes into making one of those games? How do we check if a ball collides with another one, or the boundary of the table? In the next section we'll talk a little about why collision detection is a difficult problem, followed by a little section about how video games approach collision detection. The video game example is relevant because it illustrates an important optimisation that we can make to speed up our packing sketches.
Strategies for Collision Detection
Collision detection is a difficult problem to solve due to the countless number of shapes that an item could possibly have. Shapes can range from simple circles and squares to something much more complicated like a convex polygon with an arbitrary number of sides, and mathematically it’s tricky to determine if two such shapes have overlapping or intersecting areas. To effectuate such a collision check you would have to define rules for every single way that two shapes could potentially intersect. This check would have to consider their orientation and shape, and finding a set of rules that can do this is just not straightforward, or even possible in some cases. There are just too many ways that two shapes could technically collide. This will become clearer as we have a look at some examples and solutions.
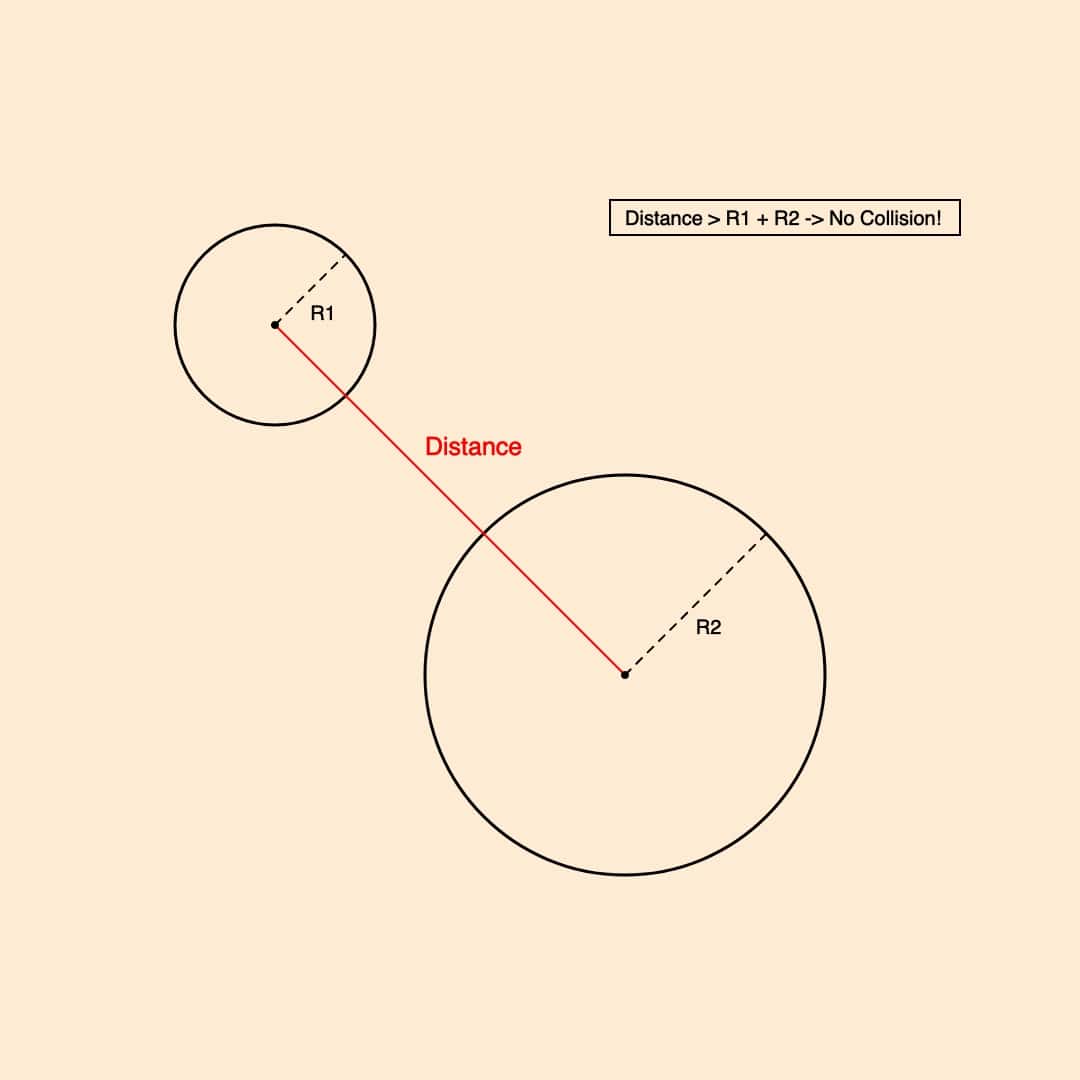
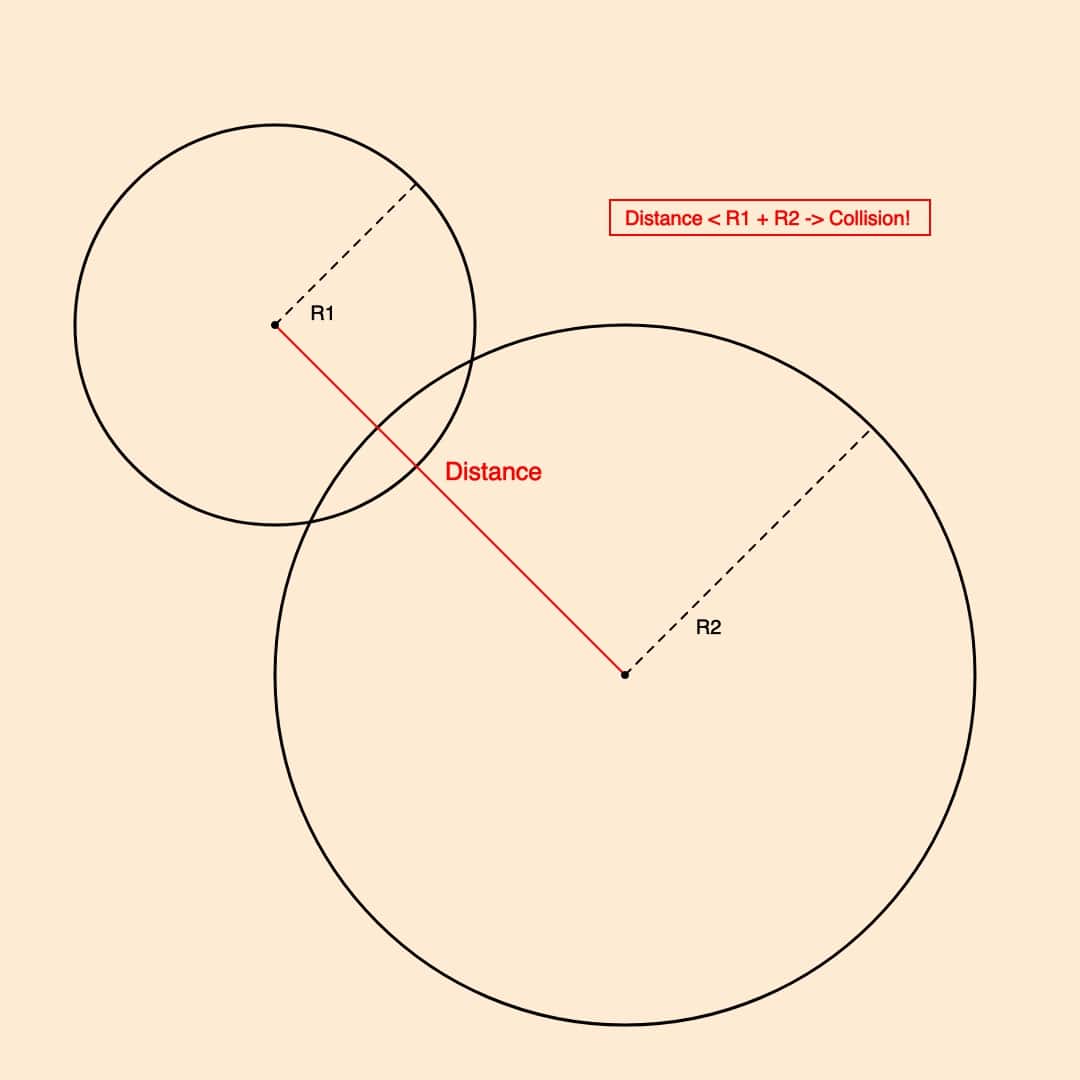
One of the simplest types of collisions to compute is that between two circles (or spheres if we're in 3D). This can be done by simply checking if the distance between their centers is less than the sum of their radii. This is the fundamental rule upon which you can build a circle packing algorithm and probably the reason why circle packing sketches occur with an overwhelming abundance in gen-art. A circle packing algorithm in this sense would attempt to iteratively place circles of various sizes on the canvas all the while checking if they ‘collide’ with any of the other circles that have already been drawn to the canvas. It is important to point out that this can become quite slow as the number of circles increases because for each circle we need to check if it collides with any of the other circles. Worth mentioning here again that this illustrates why we need some sort of smarter data structure to keep track of the shapes we've packed as the number of collision checks grows quadratically to the number of shapes that we've added if we're approaching it in a brute force manner. This is a common problem with many algorithms, and also many sketches in creative coding could benefit from this type of optimization. We’ll have a look at a solution later on. For starters, here's a very simple circle packing sketch:
To go on a little tangent here, instead of predetermining the circle’s size we could alternatively select random positions and grow our circles outward until they hit another circle. This approach is discussed in this coding train video:
Increasing the difficulty a little bit, a more complicated example is the intersection of two rectangles. The advantage of that circles and spheres have over rectangles and boxes is that they're invariant to rotation, which can not be said about rectangles. Checking collisions between rectangles is relatively easy when both of them are axis-aligned, meaning that both of them are oriented in the same manner as the x and y coordinate axes, and in simpler words tells us that they're not rotated. We would just have to check if the positional coordinate of one of them is within the area of the other, which amounts to one check per axis (2 checks in 2D). This becomes much more difficult however when they’re not axis aligned, in this case, they can be overlapping in all sorts of ways, with one corner protruding from the other rectangle.
Now let’s assume we’re dealing with a scene containing all sorts of shapes: circles, rectangles, triangles, and other polygons. Let’s also add here that these shapes can have any random orientation. We would need to define a set of rules for each pair of these shapes, which just makes it an incredibly difficult task, especially since there are so many ways that two objects can touch, overlap, and intersect. Defining intersection rules between simple geometric shapes like circles, rectangles, and triangles is probably still manageable, but how would you do it for two arbitrarily shaped polygons? The next section takes a peek at how physics engines in video games solve this problem.
Collision Detection in Video Games
If you’re a gamer, then you’ve probably at least once in your life had the thought ‘those were some bullsh*t hitboxes’. Hitboxes in video games, are essentially invisible collision boxes, you’ll also often hear the term bounding box, which essentially means the smallest enclosing box that contains a particular object (or set of points). These invisible collision boxes often only approximate the shape of 3D objects in the game world, which in turn causes collisions to not always be incredibly accurate. This sometimes leads to frustratingly unwarranted hits, even when it appears that items haven't touched, and can adversely also lead to instances where items seem to have most certainly touched without any hit being registered.
The most no-brain solution for solving collision detection is probably drawing an invisible circle underneath a given shape, roughly approximating its collision boundary. In that manner we would just need to check if the collision circles of two items overlap. However this is pretty bad actually, because you’ll often end up with a lot of wasted space in between items when you’re dealing with shapes that aren’t very circular. Imagine a long and skinny shape, the bounding circle would be enormous. We can do better than this, and we'll take some inspiration from physics engines in video games for that purpose. Rectangular boxes are usually a much better fit.
Physics engines in video games often need to balance between accuracy and performance. Generally, collision detection procedures are split into two phases, a ‘broad’ preliminary phase that yields shapes that are closely positioned on the canvas and could potentially be colliding, followed by a ‘narrow’ phase that doubles down on the results of the broad phase and checks if two objects are really touching. For 2D purposes, AABBs, short for Axis-aligned bounding boxes, which we've already discussed earlier are very popular for determining collisions in the broad phase, as they provide a cheap way to roughly estimate if two items are colliding. Additionally, we can throw a space partitioning algorithm on top of this broad phase so that we don’t have to check each shape against all of the other shapes, there isn't really any point in doing a collision check if things are on opposite ends of the screen. As for the narrow phase algorithm a popular choice is the SAT algorithm, short for Separating Axis Theorem, which can accurately determine if two convex polygons intersect. McroPixel has one of the best visual explanations of this:
I’m not going to go too deep into this because we’re not trying to build a full-blown physics engine, but rather a packing procedure that can be extended to arbitrary shapes, and which doesn’t have to run in real time. For a really good explanation adn tutorial about all of the things I mentioned above check out Nilson Souto’s wonderful post, which helped me understand these concepts.
Proposed Solution

The solution here, basically is that everything can be trivialized to a circle packing problem. Even if we’re dealing with non-circular shapes, we just need to find a way to represent the shapes at hand with a bunch of circles. This can either be done by algorithmically tracing a shape’s outline by many small circles similar to what Amy did in her Mapland’s sketch, by manually defining those positions in a photo editing software like Tarwin did in the initial version of his fruit salad packer, or by using a more elaborate method like in Tarwin’s improved version that uses ray-casting to automatically fill a transparent png with circles. Tarwin's ray-casting code is a bit outside the scope of this post, so we'll limit ourselves to tracing simple geometric shapes algorithmically.
First things first, above I have already shown a circle packing sketch, and we mentioned that it is relatively slow due to it requiring to check all of the other circles before it can place the current circle at an empty spot. We can accelerate this by utilising the space partitioning strategy similarly to what Tarwin uses in his CirclePacker library, which essentially splits up the canvas into a grid on which we will operate, such that instead of having to check circles on the entire canvas, we just need to check circles that fall into the cell that we're trying to insert into, and possibly also it's neighbouring adjacent cells.
The main optimisation is having a grid lookup - coming from the games space it just made sense to me. [...]
For this space partitioning approach we require a grid-like data structure, where each cell has knowledge of which circles it contains, and each circle has knowledge of which grid cells it falls into. This makes the objects involved a bit more complicated to manage, and has a larger memory overhead. This overhead is incomparable however in comparison to the speed improvements we obtain. In this manner we only need to check for collisions with circles that fall into any of the tiles that the to-be-placed circle is touching, this makes the entire procedure magnitudes faster. To insert composite shapes (that are composited from multiple circles), we then only need to check if all the circles that make up a shape can be placed or not, if only one of them collides with a circle on the canvas, we need to try again. This is easier said than done however, let's tackle the code in the next section.
A closer look at Tarwin's Circle Packing Library
Tarwin's sketch uses an object called circlePacker that handles everything we described in the previous section with a few useful member functions. Let's have a look at how this works by first creating the circlePacker object and it's member variables:
// the circlePacker object
function makeCirclePacker(wid, hei, gridDivs, gridPadding) {
// width and height of the circle packing area
this.wid = wid
this.hei = hei
// gridDivs (grid divisions) number of cells we want to split the grid into
this.gridDivs = gridDivs
// spacing between circles
this.pad = gridPadding
// actual size of the grid cells
this.gridSizeX = this.wid / this.gridDivs
this.gridSizeY = this.hei / this.gridDivs
// array that will contain all of the circles that we'll pack
// as well as other shapes composited out of circles
this.items = []
/*
function that creates the grid, essentially a 2d array
each cell is an object that holds it's x and y coordinates
as well as an array that contains all the circles that exist in this cell
*/
this.generateGrid = function() {
const grid = []
for (let x = 0; x < this.gridDivs; x++) {
grid[x] = []
for (let y = 0; y < this.gridDivs; y++) {
grid[x][y] = { x, y, c: [] }
}
}
this.grid = grid
}
// we still need to call the grid creation function
this.generateGrid()
}
For clarity's sake I've added a comment to each line that explains what it does and what it is used for. The grid essentially consists of a 2d array of objects, each of which knows it's own x and y coordinates, and additionally holds an array 'c' of all the circles that it contains. This grid structure will greatly facilitate and lessen the number of collision checks that we need to do while inserting a new circle.
As for the functions we've got a couple, the most important probably being the calculation of the distance between two circles. For this we can use p5's inbuilt dist() function. We can also pre-emptively subtract the sum of the radi of the two circles, meaning that we later just need to check if the result is negative or not to see if the circles touch:
// utility to check distance between two circles
this.circleDistance = function(c1, c2) {
return dist(c1.x, c1.y, c2.x, c2.y) - (c1.r/2 + c2.r/2)
}
Following this we need two fetcher functions. Firstly we require a function which, given a coordinate, can fetch the grid cell this coordinate falls into, this is needed to see which tile a circle is contained in:
// given an x and y coordinate, returns the grid cell it falls into
this.getTile = function(x, y) {
return this.grid[floor(x / this.gridSizeX)][floor(y / this.gridSizeY)]
}
Because a circle can technically touch multiple grid cells, we also need a function that can fetch all of those cells:
// gets tiles that are touched by a certain circle
this.getGridTilesAround = function(x, y, r) {
const tl = [
floor((x - r - this.pad) / this.gridSizeX),
floor((y - r - this.pad) / this.gridSizeY),
]
const br = [
floor((x + r + this.pad) / this.gridSizeX),
floor((y + r + this.pad) / this.gridSizeY),
]
const tiles = []
for (let i = tl[0]; i <= br[0]; i++) {
for (let j = tl[1]; j <= br[1]; j++) {
if (i < 0 || j < 0 || i >= this.gridDivs || j >= this.gridDivs) continue
tiles.push(this.grid[i][j])
}
}
return tiles
}
And to put it all together we need a function that actually attempts to add new circles. The function here is called tryToAddCircle because it also takes in an optional parameter called actuallyAdd. We can use this function to either simply check if a circle fits, or to actually add that circle and grow it until it's occupying the most space it can.
// function that attempts to add a circle
this.tryToAddCircle = function(x, y, minRadius = 5, maxRadius = 200, actuallyAdd = true) {
// create a new object that represent a new circle
let c1 = { x, y, r: minRadius, t: [] }
while (true) {
// break early if outside the circle packing area
if ( c1.x - c1.r < 0 || c1.x + c1.r > this.wid || c1.y - c1.r < 0 || c1.y + c1.r > this.hei ) {
return null
}
// Get grid cells that the to-be-placed circle touches
const gridTiles = this.getGridTilesAround(x, y, c1.r)
// Check against other circles in these tiles
for (let tile of gridTiles) {
for (let c2 of tile.c) {
// get distance between circles
const d = this.circleDistance(c1, c2)
// check if this distance is negative ( minus padding )
// this means a collision was registered
if (d - this.pad < 0) {
// if there was a collision and the circle size is still minimum
// there is no space for the circle to grow so we discard and try again
if (c1.r === minRadius) {
return null
} else {
// if the circle had a collision and has grown already
// we either add it or return depending on the actuallyAdd toggle
if (actuallyAdd) {
// add to tiles, and tiles to circles
gridTiles.forEach(t => {
this.grid[t.x][t.y].c.push(c1)
c1.t.push(`${t.x},${t.y}`)
})
this.items.push(c1)
}
return c1
}
}
}
}
// grow the circle radius
c1.r += 1
// if we reach maximum radius size we either add it
// or return it
if (c1.r > maxRadius) {
if (actuallyAdd) {
// add to tiles, and tiles to circles
gridTiles.forEach(t => {
this.grid[t.x][t.y].c.push(c1)
c1.t.push(`${t.x},${t.y}`)
})
this.items.push(c1)
}
return c1
}
}
}
This function looks intricate but it's flow is straight forward really. This function takes as input an x and y coordinate, a minimum and maximum radius and an optional boolean parameter called 'actuallyAdd'. When actuallyAdd is set to false we will not actually create new circles, we will simply check if a circle can fit in a certain position, and how much it can grow it's radius before it collides with another circle.
We create an object to represent the current circle that we're attempting to place. In a while loop we need to do a few things, the first of which is fetching all of the grid cells that this circle intersects. We will need to loop over all of the circles within those tiles and check if our current circle collides with any of them. There are a couple of outcomes:
- We register a collision while the circle is still at minimum radius. This means that the circle has not grown and there is no room for it to grow. We can break the while loop, return and try again with other coordinates.
- We register a collision and the circle has a radius larger than the minimum radius that we've specified. If the actuallyAdd toggle is true, we need to do a couple of things. We add the circle to the circle arrays of all the tiles it falls into, add the tiles it touches to it's own tile array, and we also add it to the array of packed items of the circlePacker class.
- If no hit is registered and the circle keeps growing, we stop when it reaches a maximum circle size and again if the actuallyAdd toggle is true we need to update the appropriate arrays.
In case the actuallyAdd toggle is false we just return the circle object if it can be placed, and null otherwise. This will come in handy in the next section. Now this is really efficient, go ahead and try it for yourself, first run the circlePacker with with the gridDivs parameter set to 1 and then again run it with it set to 100. Now slowly ramp up the circle count for both, you'll quickly see that with a finer gridDivs number it's way faster!
Generalizing for Other Shapes
Now what Tarwin has setup so far is a great chunk of code, because generalizing it for other shapes is only a little step away. We already discussed that we simply need to composite a shape out of several smaller circles that trace out it's form, or alternatively it's outline, to be able to pack it. In this manner we just need to check if all the circles that make up this shape are 'addeable' according to our circle-packing procedure. For this we will reuse the tryToAddCircle method in a loop and this time actually pass false as the actuallyAdd input parameter. In this manner, if any one of the checks fails we terminate the function and need to try again:
// function that checks if a shape can be placed
tryToAddShape(circles, actuallyAdd = true) {
// 'circles' here is the array of circles that makes up a specific shape
for (let c of circles) {
if (!this.tryToAddCircle(c.x, c.y, c.r, c.r, false)) {
// if one of these circles can't be placed we return
// shape can't be placed
return null
}
}
// if there were no problems then we can safely add all circles
if (actuallyAdd) {
circles.forEach(c => this.addCircle(c))
}
return circles
}
To actually add the circles of the shape we require another function that simply adds the circles (second part of the tryToAddShape function):
this.addCircle = function(c) {
// Break early if out of grid
if (c.x - c.r < 0 || c.x + c.r > this.wid ||
c.y - c.r < 0 || c.y + c.r > this.hei
) {
return null
}
// Get grid cells it intersects
const gridTiles = this.getGridTilesAround(c.x, c.y, c.r)
// Update appropriate arrays
gridTiles.forEach(t => {
this.grid[t.x][t.y].c.push(c)
if (!c.t) c.t = []
c.t.push(`${t.x},${t.y}`)
})
this.items.push(c)
return c
}
Compositing Shapes with Circles
With the previous code in place, we can now actually create a shape made out of circles. Let's have a look at an example, we'll be creating a rectangular shape:
// function that makes a rectangle from circles adapted from Tarwin's 'Shape' class
function makeRectangularShape(sizeW, sizeH) {
this.original = [] // original unmodified circles
this.circles = [] // circles after scaling, rotating and translating
// dimensions of the rectangles
this.sizeW = sizeW
this.sizeH = sizeH
// Create circles that trace outline of the rectangle
// This is a bit backhanded with trigonometric functions
// https://math.stackexchange.com/a/279209/673569
this.makeOriginal = function() {
for (let a = PI / 4; a < TAU + PI / 4; a += TAU / 4) {
// a vertex of the rectangle
let ax = this.sizeW * Math.sign(cos(a)) / 2
let ay = this.sizeH * Math.sign(sin(a)) / 2
// the next vertex of the rectangle
let axn = this.sizeW * Math.sign(cos(a + PI / 2)) / 2
let ayn = this.sizeH * Math.sign(sin(a + PI / 2)) / 2
// interpolate between them (can be improved)
// basically increase number of steps the longer the edge length is
for (let inter = 0; inter < 1; inter += .02) {
let xi = ax * inter + axn * (1 - inter)
let yi = ay * inter + ayn * (1 - inter)
// push circle to original
this.original.push({x: xi, y: yi, r: this.sizeW/24})
}
}
// copy original into circles
this.circles = this.original.map(c => ({
...c
}))
}
// scale, rotate and translate
// function that's used to actually place the shape
this.scaleRotateTranslate =
function(scale, rotateRadians, translateX, translateY) {
// reset circle array
this.circles = []
// apply transforms and re-add
this.original.forEach(c => {
const x = c.x * scale
const y = c.y * scale
const r = c.r * scale
// rotate and translate each x and y
const x2 = x * cos(rotateRadians) - y * sin(rotateRadians) + translateX
const y2 = x * sin(rotateRadians) + y * cos(rotateRadians) + translateY
this.circles.push({ x: x2, y: y2, r })
})
}
}
Shapes will consist of object that hold two member functions. The first of which is responsible for creating the circles that trace the shape, whereas the second takes care of positioning and transforming the shape. The latter is required to pack a multitude of different variations of the same shape.
Making rectangles, as opposed to squares, with trigonometric functions is a bit tricky. Due to their width and height not being the same we need to use a set of parametric functions that make use of the sign of cos() and sin(). It could be done in an easier manner by defining the corner points of the rectangle and then spanning circles between those. As for the scaleRotateTranslate function, it's shape agnostic. It will simply take the original circles and apply the transforms according to the input parameters we've passed.
The Shape Packing Procedure
The final piece of the puzzle is to define the shape packing procedure. This is somewhat similar to the tryToAddCircle function, with a few changes.
// We need to declare a few global parameters that will determine the look of our sketch
const MIN_SCALE = 5
const MAX_SCALE = 300
const SCALE_INCREMENT = 0.1
const NUM_ITEM_PLACE_TRIES = 200000
function packShapes() {
for (let i = 0; i < NUM_ITEM_PLACE_TRIES; i++) {
// set the shape to have a minimum size
let currentScale = MIN_SCALE
// random coordinates
let x = random(w)
let y = random(w)
// random rotation
let rotateRadians = random(TAU)
// We need these two variables to determine
let lastAdded = null
let lastAddedImage = null
// random rectangle dimensions
let randW = random(1,15)
let randH = random(1,15)
// let's assume we have two types of shapes rectangles 'R' and triangles 'T'
let type = random(['R','T'])
let currentShape = (type=='R')?new makeRectangularShape(randW, randH):new makeTriangularShape(randW);
// create it's original circles
currentShape.makeOriginal()
while (currentScale < MAX_SCALE) {
currentShape.scaleRotateTranslate(currentScale, rotateRadians, x, y)
const added = circlePacker.tryToAddShape(currentShape.circles, false)
if (!added && !lastAdded) break
if (!added && lastAdded) {
lastAdded.forEach(c => {
circles.push({ x: c.x, y: c.y, r: c.r })
})
lastAdded.forEach(c => circlePacker.addCircle(c))
shapes.push(lastAddedImage)
break
} else if (added) {
lastAdded = [...added]
lastAddedShape = {
type: type,
x: x, y: y,
scale: currentScale, rotation: rotateRadians,
sizeW: randW, sizeH: randH,
triangleSizes: (!currentShape.sizeParam)?0:currentShape.sizeParam
}
}
currentScale += SCALE_INCREMENT
}
}
}
In this shape packing function, similarly to the tryToAddCircle function, we're trying to grow shapes starting from a minimum scale. We use two variables added to keep track of each shape, and decide if it can or cannot be placed. In a while loop we attempt to add the shape via the tryToAddShape function, if it can be added it will return an array of of circles, which makes the added variable truthy. If it is not possible to add the shape the tryToAddShape function will return null, which is faulty. In this case if lastAdded is also still null it means that the shape is at minimum scale and can't grow, which indicates that the location is not a good fit. Hence we break and try again. We resume similarly to the the tryToAddCircle function. If added is falsy but lastAdded is truthy it means that the shape has in fact grown, in that case we can terminate the function and add the shape, by adding all of the circles it is made of. We also need to store the positional and transform information of the shape!
If added and lastAdded are both truthy, then the shape still has room to grow and we need to update the lastAdded object that stores information of the previous version of the shape.
A Complete Example
Albeit having a grid-lookup, it still takes a few moments to run the sketch, which is still better than having to wait several minutes (or hours). Here's a complete example of everything we've discussed so far:
Closing Notes
For more complicated shapes, like in Tarwin's original fruit salad sketch you have the option of compositing these circles in a photo editing software, then exporting them as array an loading them in. Alternatively you can go and give Tarwin's circle fill algorithm a look.
If you want to do real-time collision detection you’d better stick to an already established physics engine, like Matter.js that allows you to create all sorts of rigid bodies. I found it a bit difficult to fine-tune though, the bodies were a bit too elastic for my taste, but I didn't spend much time with it, so you might get better results! If you want to learn about collision detection between simple shapes and how to do it in p5js. An excellent book by Jeff Thompson on this topic.
And that's it, if you've reached here kudos to you and many thanks for reading! If you've learned something and enjoyed this post consider sharing it with your friends, giving me a follow on Twitter or IG. Thanks again for reading and happy sketching, cheers!
