Before we begin with this post, I'd like to point out that a lot of research has gone into algorithms for constructing Delaunay Triangulations. The intent of this post is solely to present a somewhat straightforward and popular method for constructing such a triangulation, as well as learning some useful techniques along the way. The Bowyer-Watson algorithm is well suited for making artworks with a moderate amount of points. For creating animated or interactive triangulations I would recommend using one of the many efficient and highly optimized libraries that already exist for these purposes like delaunator. I'll include a short section how to use the delaunator at the end!


Lastly, before we begin, you can find a highly un-optimized version of the BW algo here which was essentially my initial version of the algo. This tutorial is loosely based on Matias Savela's implementation which is quite digestible and very readable, and improves on the mistakes and implementation choices that I've made during my initial attempt! With this out of the way we can dive into the algorithm:
Before we begin
- Wikipedia's Bowyer-Watson Pseudocode Snippet
- An intuitive explanation of the algorithm
- Implementation Details
The Code
- Vertex, Edge and Triangle Classes
- The super Triangle
- The triangulation procedure
- Putting it all together
- Using the Delaunator library
Wikipedia's Bowyer-Watson Pseudocode Snippet
After digging a bit on how to approach the triangulation task I came across a pseudocode snippet on the BW wikipedia page. It loosely describes the required steps of the algorithm and I encourage you to read it until you've got a general idea, but it's not necessary, you can safely skip this section:
function BowyerWatson (pointList)
// pointList is a set of coordinates defining the points to be triangulated
triangulation := empty triangle mesh data structure
// must be large enough to completely contain all the points in pointList
add super-triangle to triangulation
// add all the points one at a time to the triangulation
for each point in pointList do
badTriangles := empty set
// first find all the triangles that are no longer valid due to the insertion
for each triangle in triangulation do
if point is inside circumcircle of triangle
add triangle to badTriangles
polygon := empty set
// find the boundary of the polygonal hole
for each triangle in badTriangles do
for each edge in triangle do
if edge is not shared by any other triangles in badTriangles
add edge to polygon
// remove them from the data structure
for each triangle in badTriangles do
remove triangle from triangulation
// re-triangulate the polygonal hole
for each edge in polygon do
newTri := form a triangle from edge to point
add newTri to triangulation
// done inserting points, now clean up
for each triangle in triangulation
if triangle contains a vertex from original super-triangle
remove triangle from triangulation
return triangulation
If you've already got a headache after reading this snippet, then fret not, things will get clearer in what follows in this post. Albeit translating pseudocode into executable code being a very good exercise, a lot of the implementation details are left for the coder to decide on. In many ways this pseudocode snippet can be further simplified. But let's first go through the algorithm step by step!
An intuitive explanation of the Algorithm
Here's a little step-by-step animation to illustrate how the Bowyer-Watson algorithm functions on a very simple set of three points. The Bowyer-Watson algorithm is essentially an iterative procedure that loops over a given set of points (placed at random or purposefully), one at a time, and constructs a valid Delaunay triangulation:
An initial and necessary first step here, to get things going, is to create a large triangle which will contain within it's three edges all of the points that ought to be triangulated. We call this triangle a 'super triangle'. We could technically make this triangle infinite in size, to make sure that all triangulation vertices are contained within it, however pragmatically we can make it just big enough to contain all of the points:
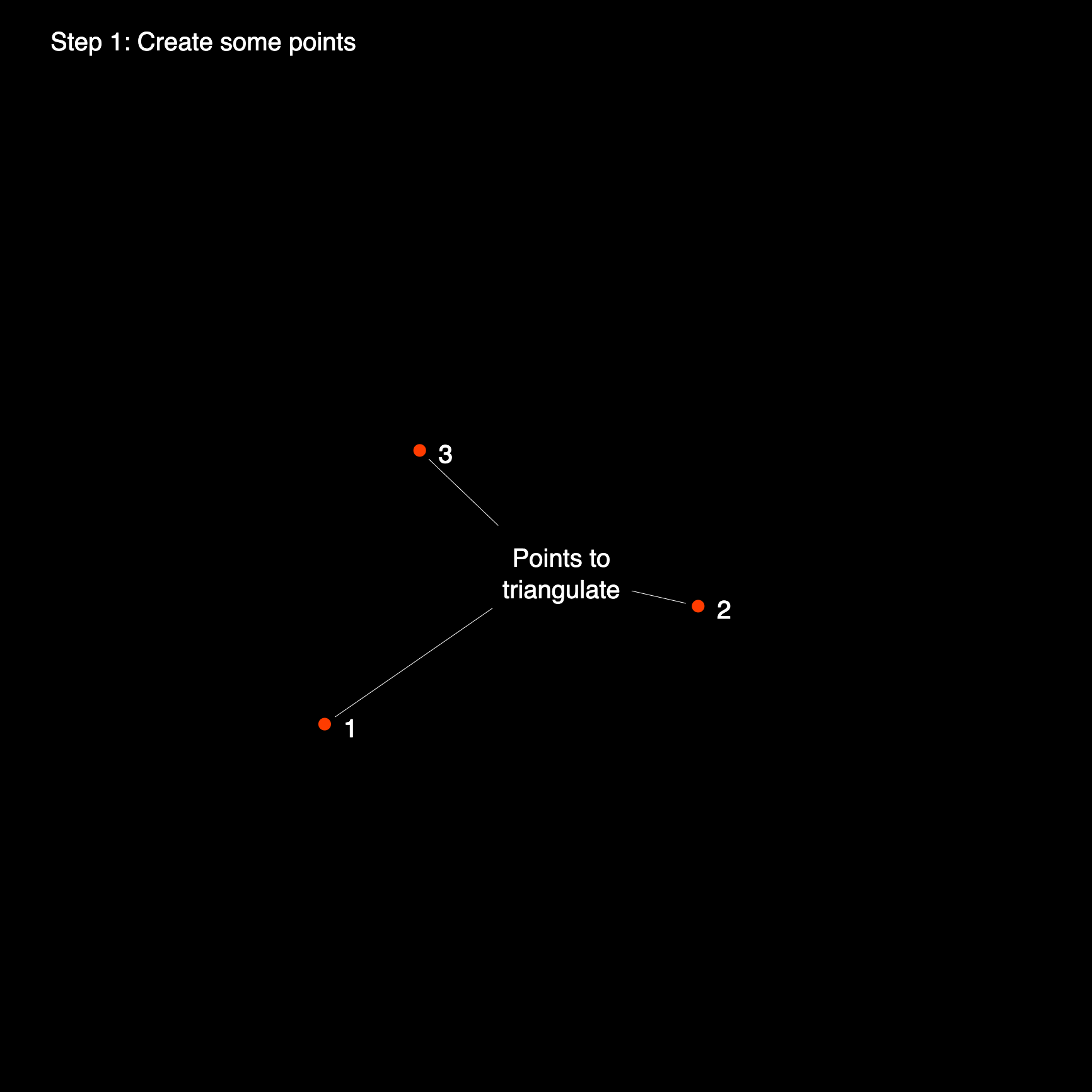
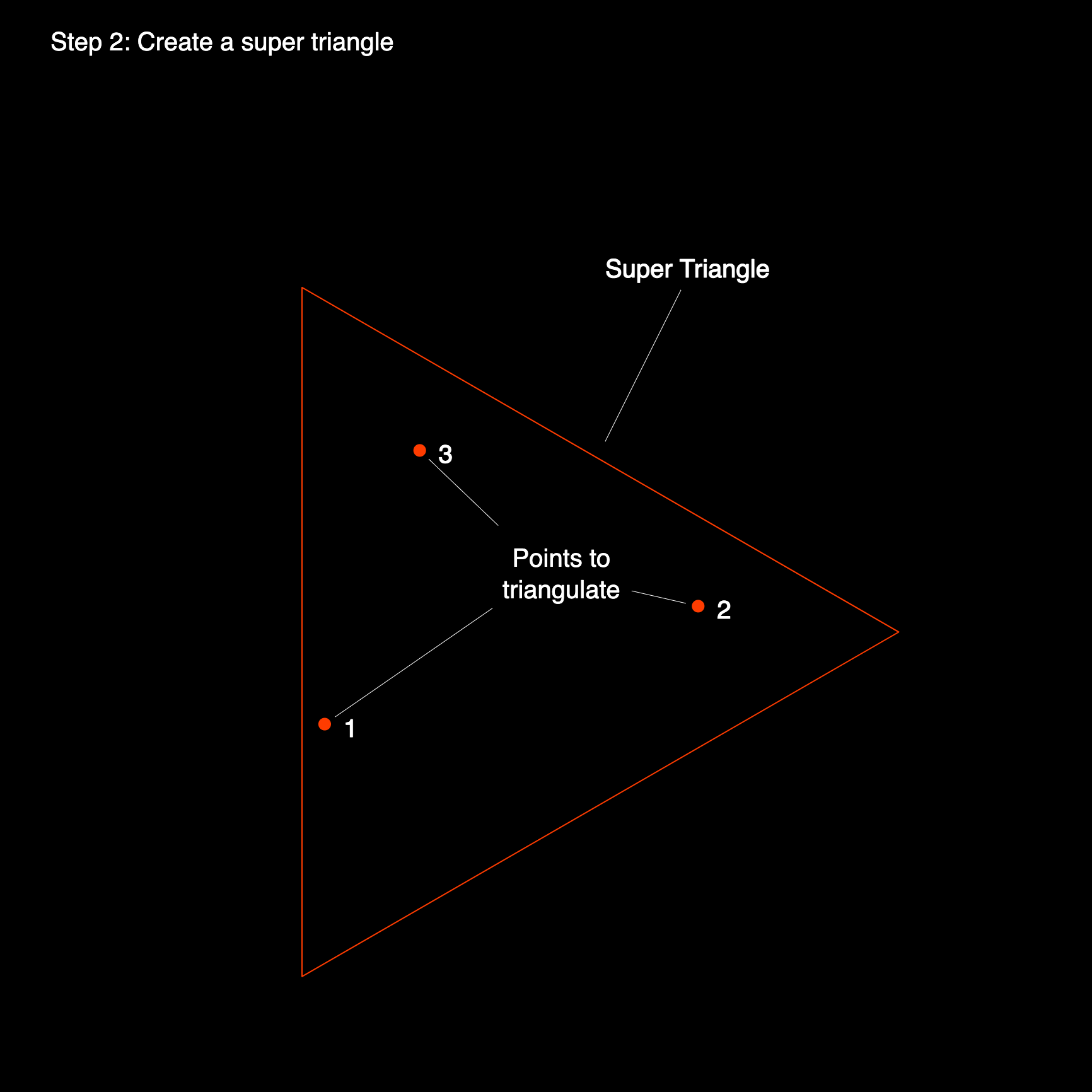
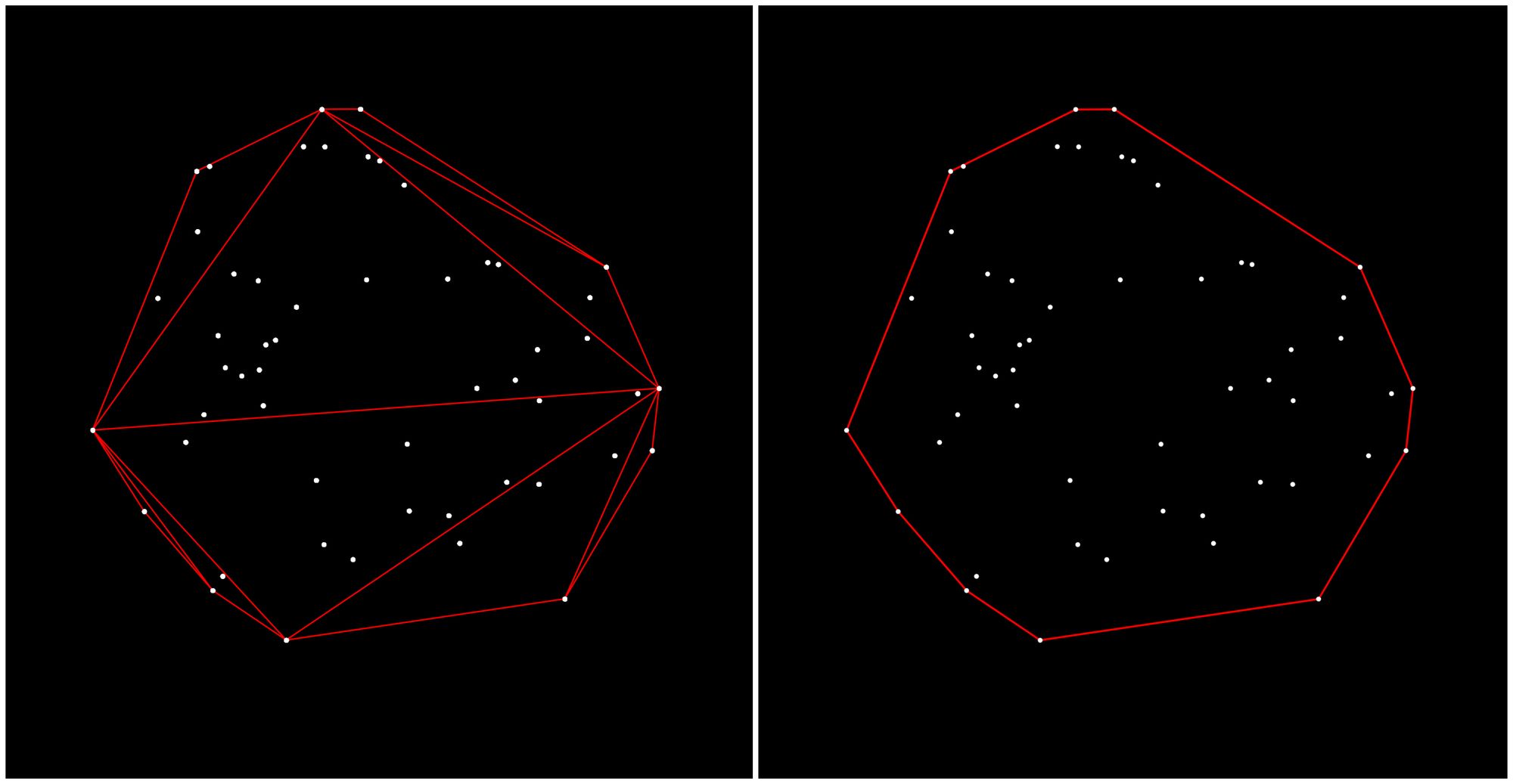
Having created this super triangle and placed our points we can begin constructing the triangulation. We will now iteratively go over each point that we have passed to the procedure to construct a valid triangulation. In the previous post we have discussed what makes a valid Delaunay Triangulation:
A Delaunay triangulation for a given set P of discrete points in a general position is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P).
Thus the next step is checking if any of our points fall within the circumcircle of any of the already existing triangles. Initially this is simple, since we only have one triangle (the super triangle), which certainly contains all of the points within it's circumcircle. We can mark this super triangle as invalid, and add it to an array that contains all of these invalid triangles. Again, we're still at the very beginning, hence the array will only contain the super triangle for now.
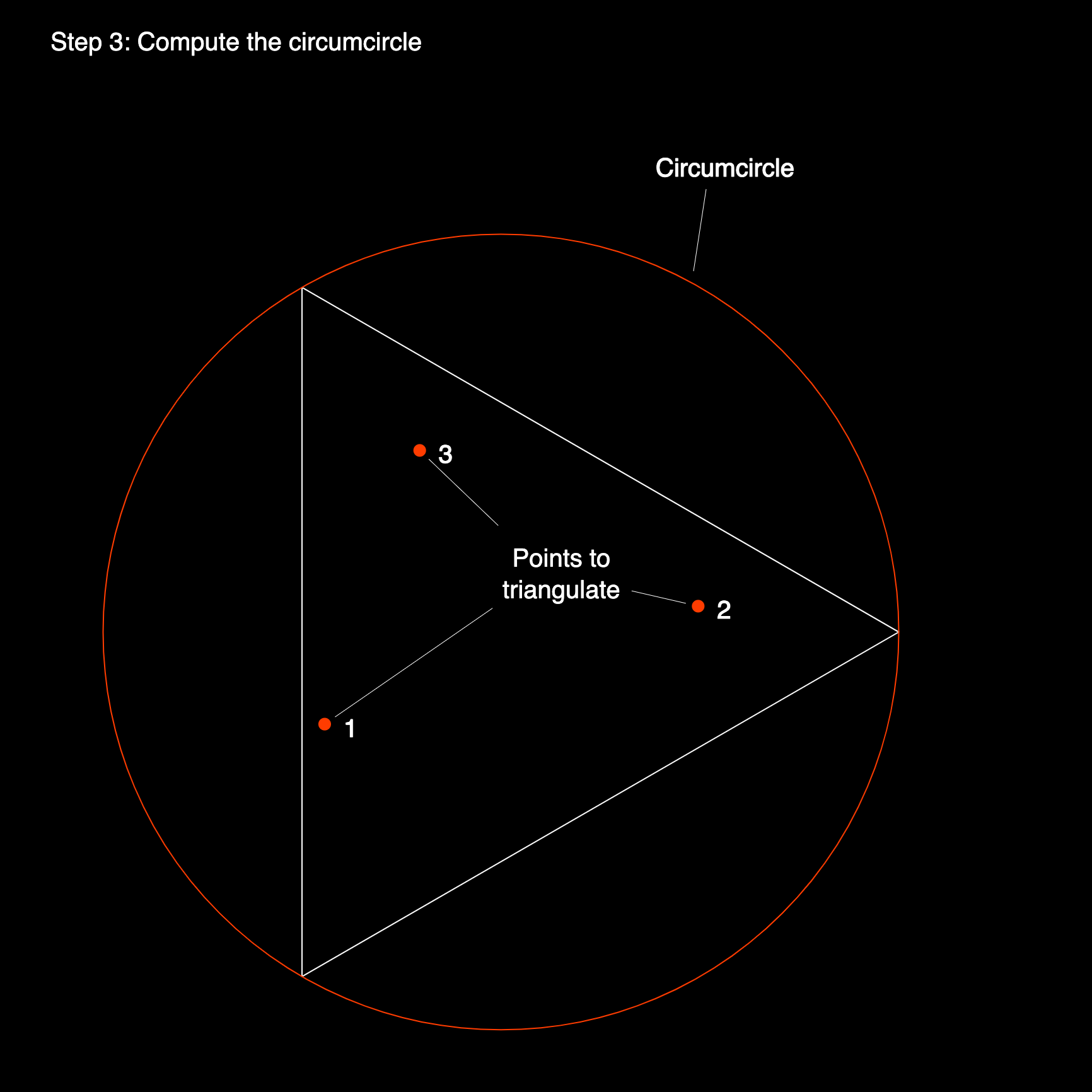
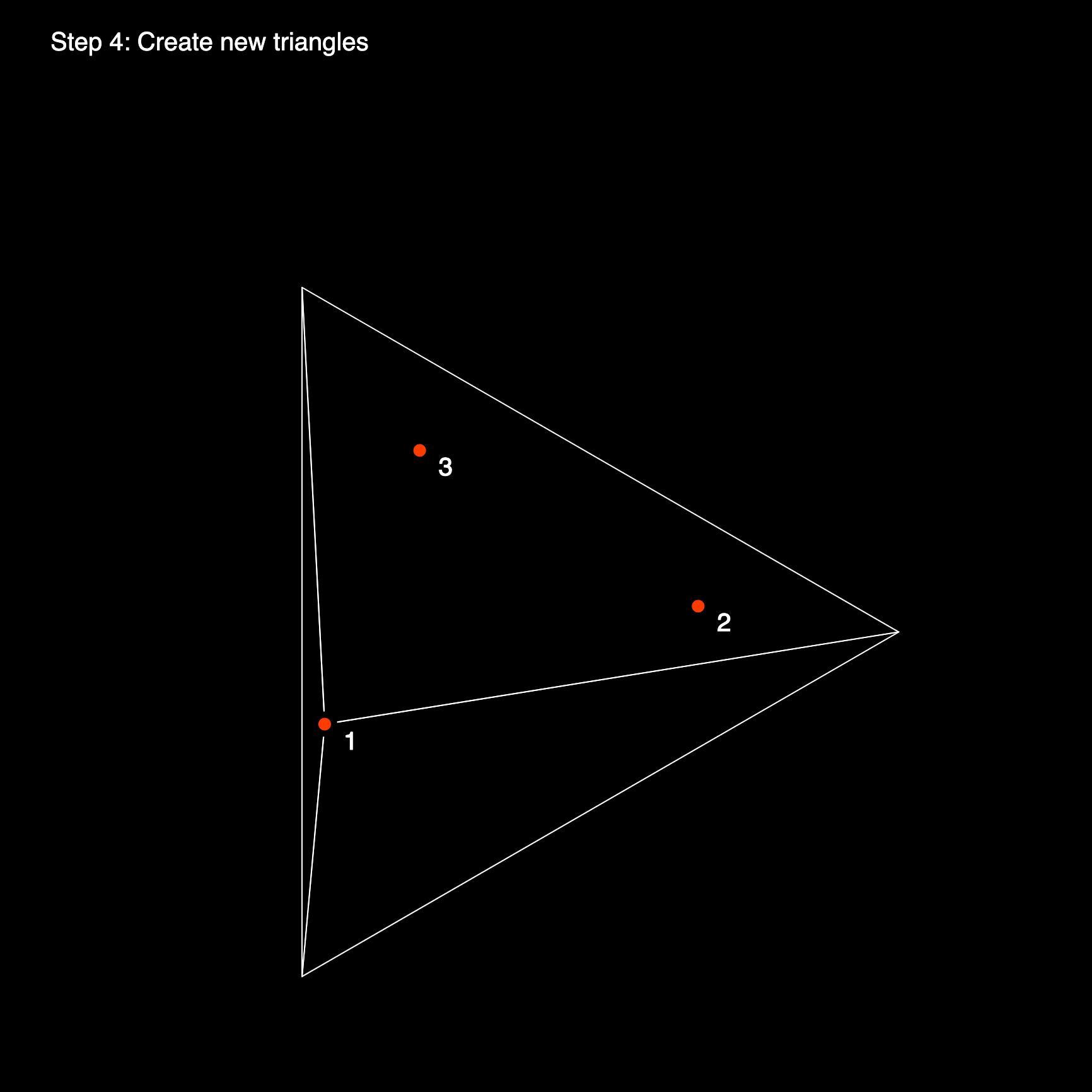
Next, we need to replace the invalid triangles by a different set of triangles that is valid. We can do so by connecting the edges of the super triangle to the initial point that we're currently iterating over. In this manner we can make sure that the point will be on the circumcircle of the new triangles, because it is a vertex of each one of those triangles.
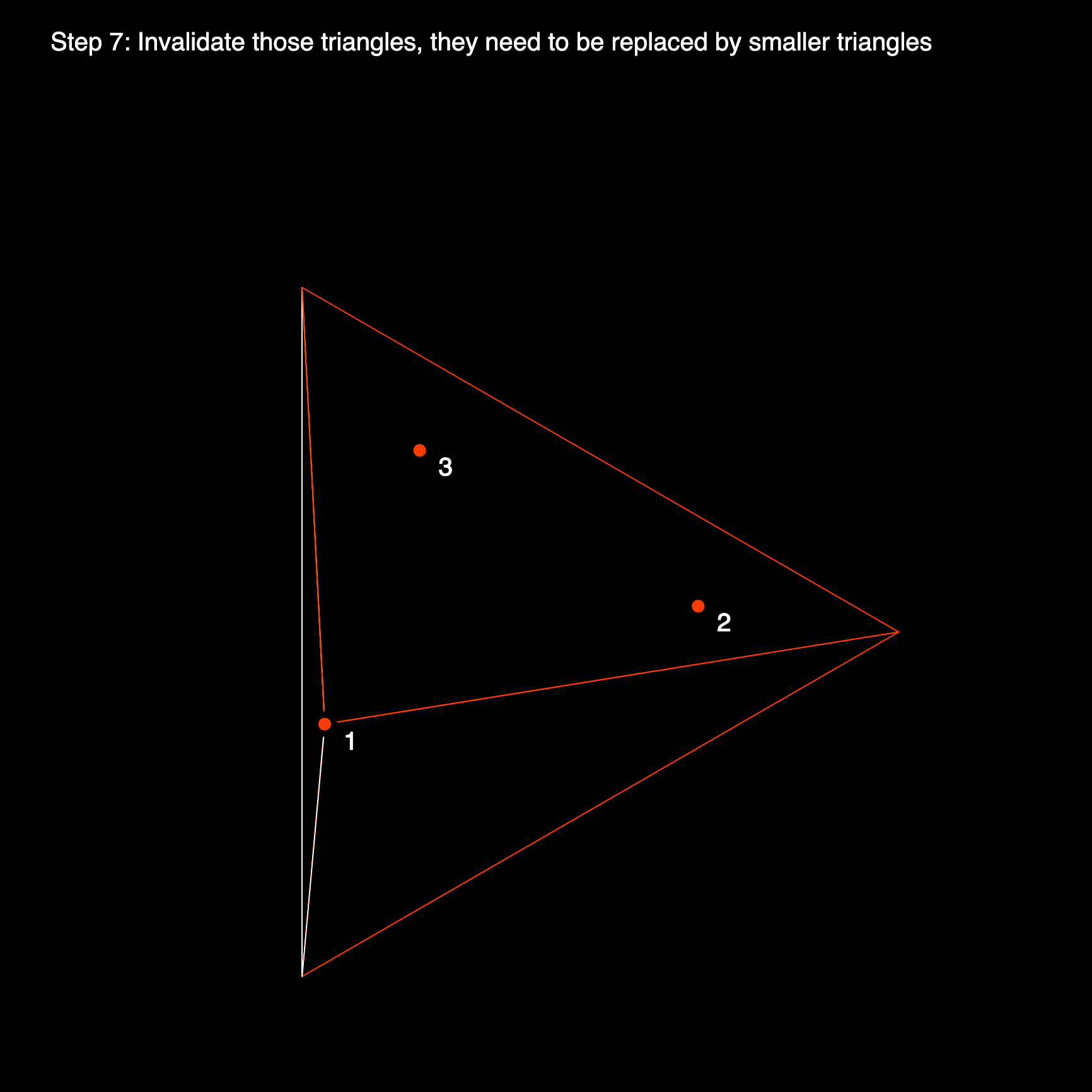
Later on this becomes trickier because we need to determine the boundaries of the polygonal hole that is formed in the triangulation where we, in most cases, marked several triangles as invalid. We essentially need to fill the empty spot where we figuratively 'deleted' the bad triangles, by connecting the edges of this polygonal hole to the current point we're iterating over.
Before we end the current iteration we still need to delete all triangles that have been marked as invalid, and add the new triangles that we've formed by connecting the point with the edges of the polygonal hole. And we are ready for the next iteration.
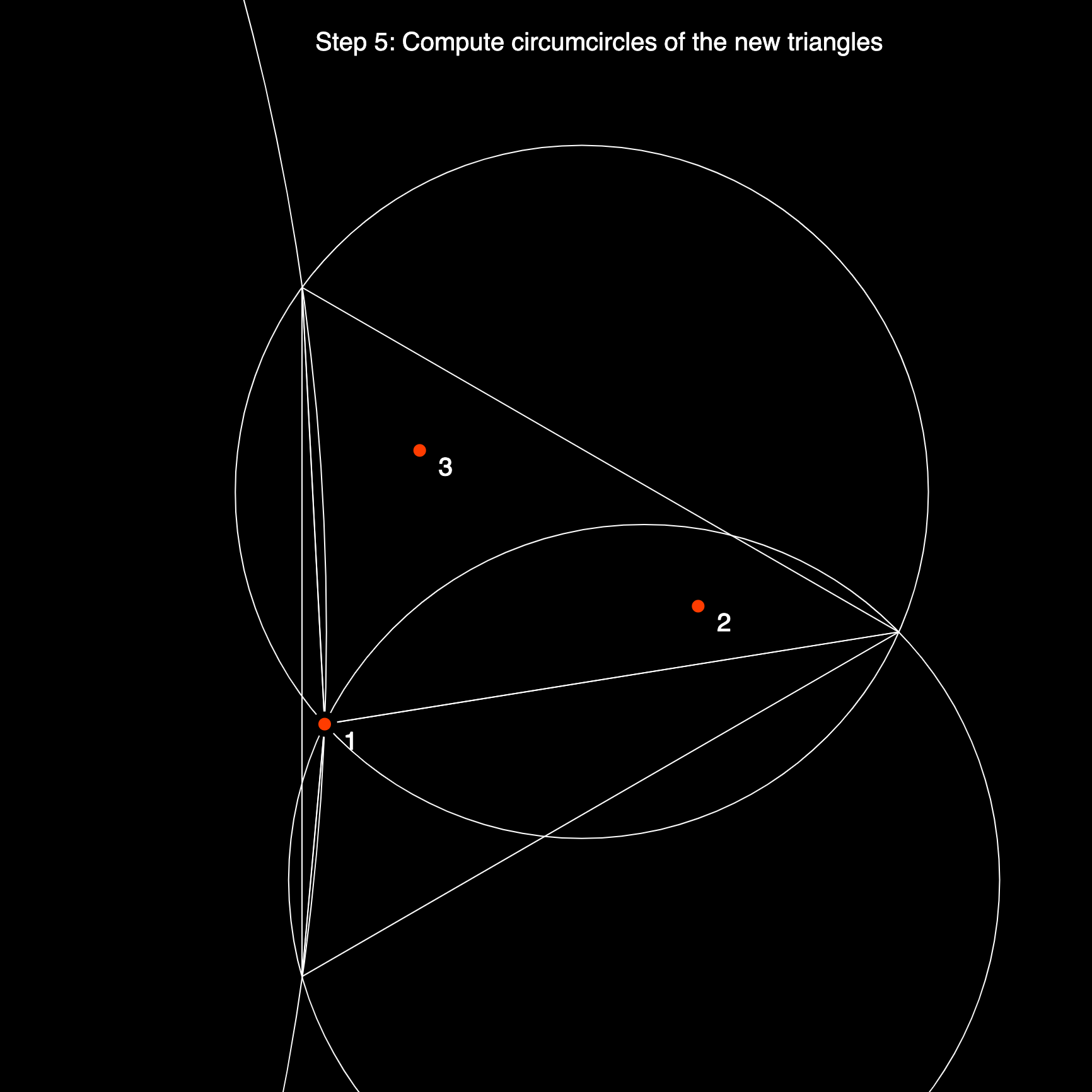
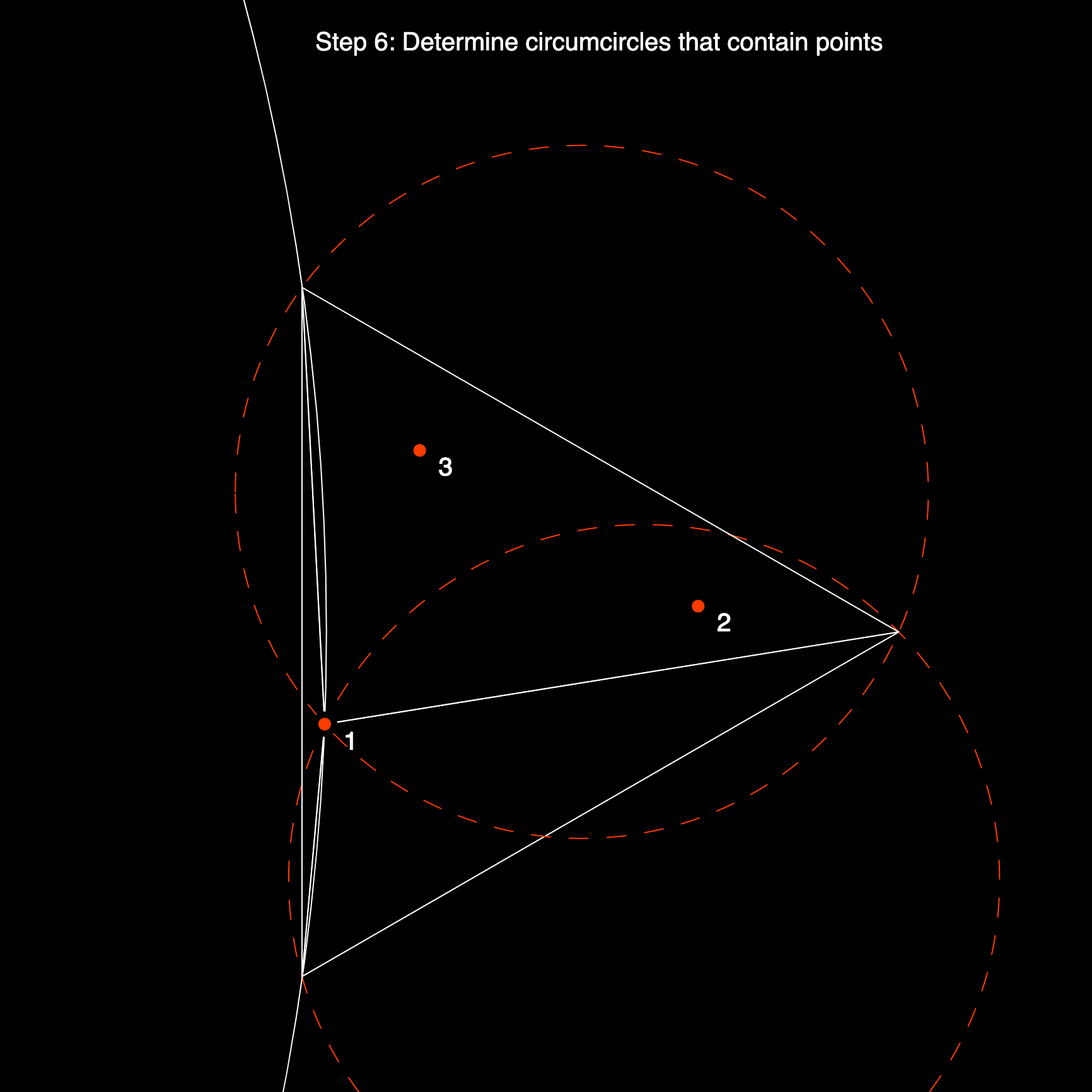
In the second iteration we will add the next point to the triangular mesh, and depending on it's position and the shape of the three triangles that we've created, it might fall into one, two or more circumcircles. If it does we need to mark those triangles as invalid, and we now need to find the polygonal hole, where we essentially deleted several triangles. The pseudocode snippet describes the polygonal hole as 'all edges in the set of bad triangles that is not shared between two bad triangles' which essentially means all the edges at the boundaries of that polygonal hole. Depending on how the code is implemented this can be more or less difficult. And again we form new triangles by connecting these unshared edges with the current point and adding these triangles to the triangulation.
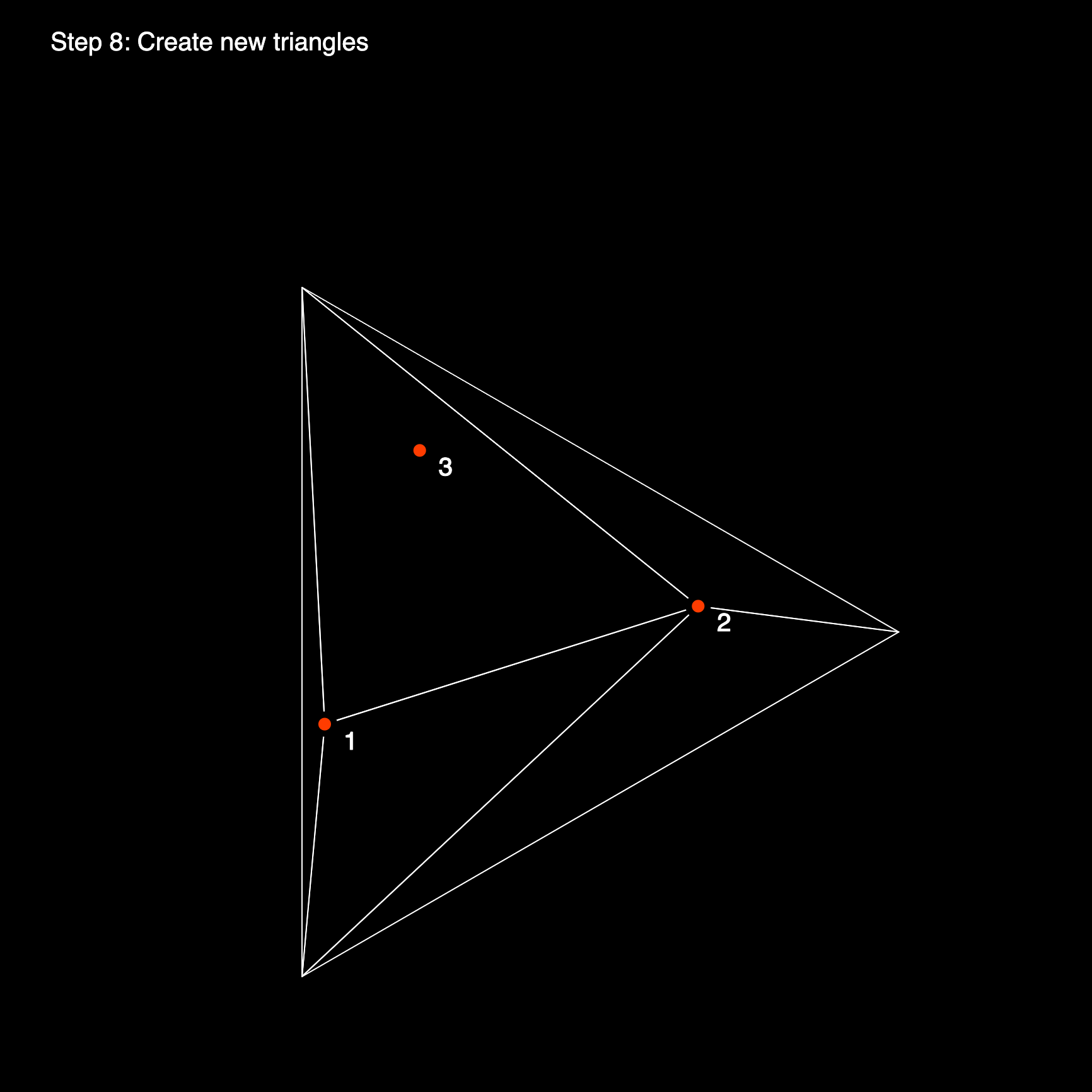
In this manner we iteratively add vertices to this triangle mesh, subdividing the initial super triangle into smaller ones, until we've ultimately achieved a valid Delaunay triangulation. In the final step we will need to remove all triangles that share an edge or a vertex with the initial super triangle, since they weren't actually part of the initial set of points.
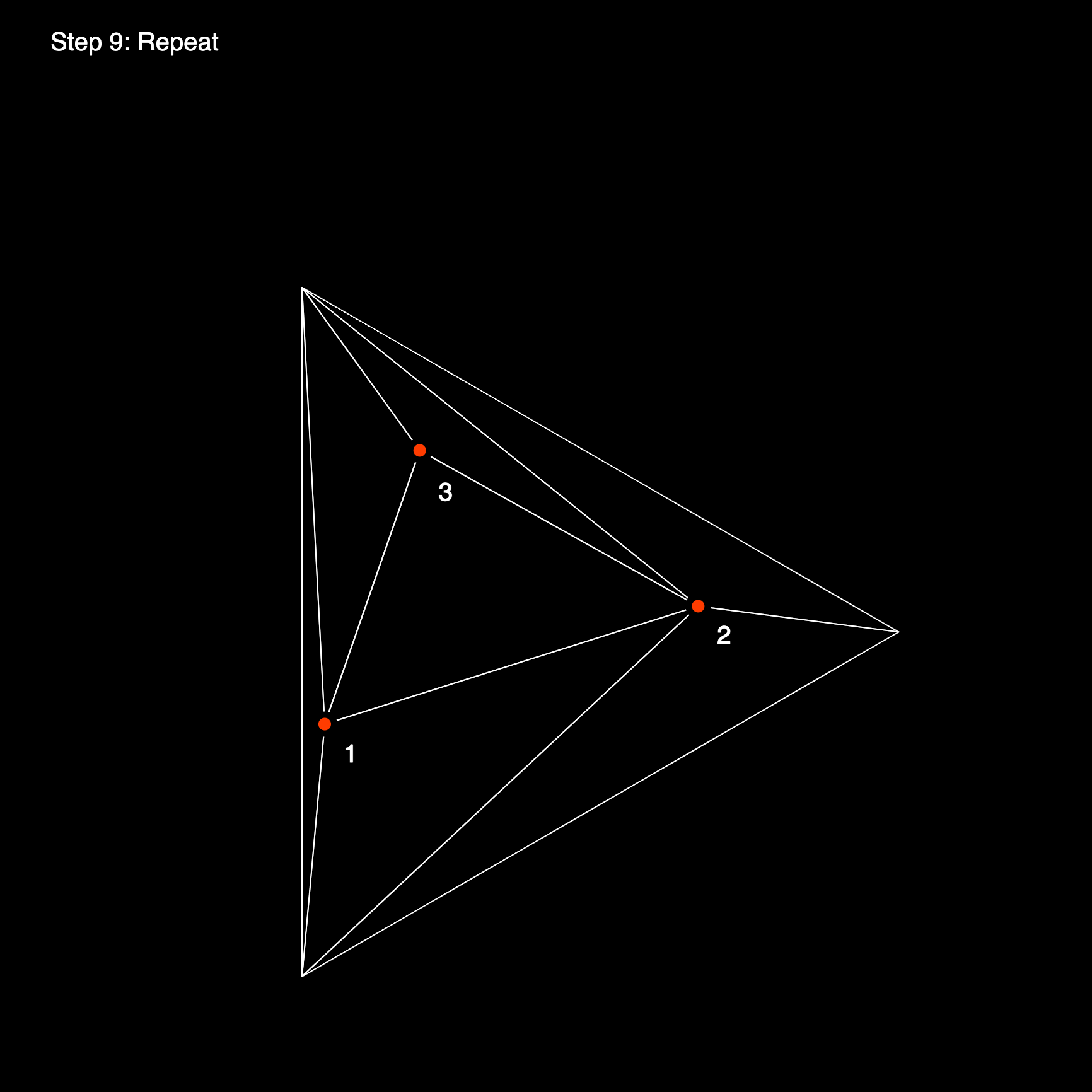
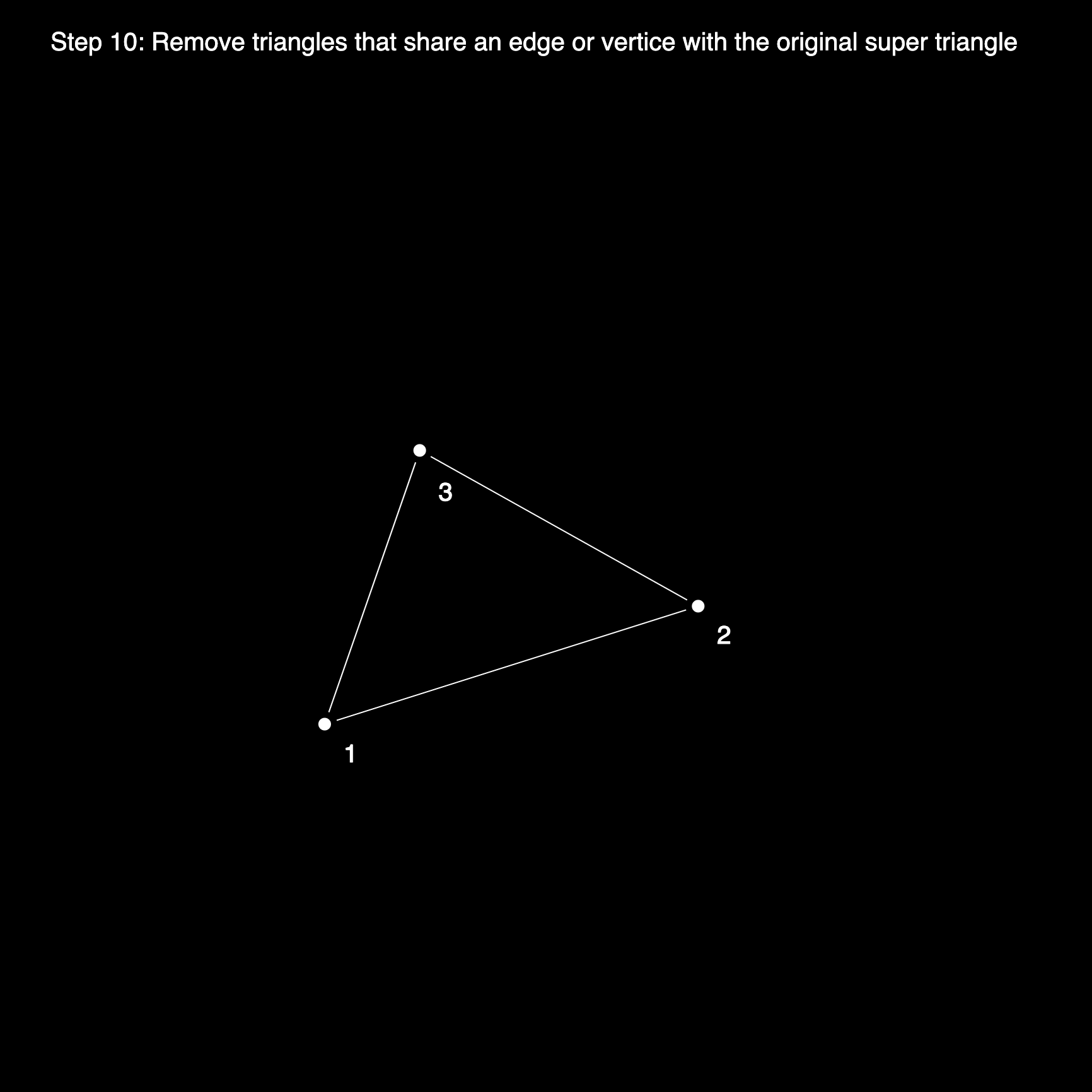
Implementation Details
As mentioned earlier, a pseudocode snippet generally only tells you the major steps, but not about the smaller sub-routines that need to be incorporated to achieve these steps. For example, we should first write some robust code that can compute the circumcenter and circumcircle of a triangle since it is one of the cornerstones of this algorithm. Equivalently, implementing the vertex, edge and triangle information in a useful manner is crucial to save us many headaches along the way, especially since we need to make a large number of edge comparisons to find the polygonal hole.
The computation of the circumcenter and circumcircle will be discussed in a different post !!! here !!! because it is an interesting geometric problem on it's own outside the context of the Delaunay triangulation. In the post there's a number of ways to compute the circumcenter.
The Vertex, Edge and Triangle Classes
Let's start with writing the classes for the major three components of the triangulation: a vertex class, an edge class and a triangle class. The vertex object being the most basic one, only consisting of an x and y coordinates as well as a short comparison function:
// Vertex object
var Vertex = function(x, y) {
this.x = x
this.y = y
this.equals = function(vertex){ return this.x === vertex.x && this.y == vertex.y }
}
The edge object builds on top of the Vertex object. In this manner an edge essentially consists of two connected points, and can thus be represented by two vertices. It also has it's own comparison function. This function actually needs to do two comparisons to determine if an edge is equivalent to another one, because for our purposes we don't really care for the cirectionality of the edges. Meaning that an edge going from vertex A to vertex B is the same as an edge going from vertex B to vertex A. Hence we need to cover both cases:
// Edge object
var Edge = function(v0, v1) {
// The two vertices that make up the starting and ending vertex of the edge
this.v0 = v0
this.v1 = v1
// Comparison function to compare this edge to another
this.equals = function(edge){
return (this.v0.equals(edge.v0) && this.v1.equals(edge.v1)) ||
(this.v0.equals(edge.v1) && this.v1.equals(edge.v0));
}
}
This could be further optimised by assigning an ID to each edge and vertex and keeping track of them in a lookup table, saving us costly and redundant comparison operations. A simply comparison should do for now however. Next up is the triangle object:
// Triangle object
var Triangle = function(v0, v1, v2) {
this.v0 = v0
this.v1 = v1
this.v2 = v2
this.circumCirc = calcCircumCirc(v0,v1,v2)
this.inCircumcircle = function(v) {
var dx = this.circumCirc.c.x - v.x;
var dy = this.circumCirc.c.y - v.y;
return Math.sqrt(dx * dx + dy * dy) <= this.circumCirc.r;
}
};
For the triangle object we don't require a comparison function (because we can compare it's edges), and the circumcenter computation we've outsourced. We just need some additional functionality to check if a given vertex is within the circumcircle of the triangle or not. Which can be done by calculating the distance from a given point to the circumcenter and checking if it less than it's radius.
The Super Triangle
This seems like a very simple part of the overall algorithm, but can also be considered an interesting problem. As said earlier, we could just make a triangle gigantic enough such that it encloses all of the points. For example, we choose all of our point coordinates to fall within the region that makes up the canvas, and then make our triangle large enough to contain the entire canvas. In that case all of the points would certainly be inside the super-triangle.
A more interesting and much more difficult method would be finding a triangle that is just large enough to contain all points. There might even be problems with the first approach as detailed here where the final triangulation doesn't end up being quite perfectly 'Delaunay'. In this sense we are looking at a minimum bounding box type of problem, and in this case it would be a minimum bounding triangle, one such algorithm that can compute this bounding triangle can be found here. But this is a bit overkill as we would first have to compute the convex hull of the set of points, which makes things overly complicated when we could simply slap a big triangle around our points.
Here's Matias' method for finding the super-triangle. His function first finds the minimum and maximum vertex coordinates and then centers a triangle on top of all the points:
// Triangle that bounds given vertices
var superTriangle = function(vertices) {
var minx = miny = Infinity,
maxx = maxy = -Infinity;
vertices.forEach(function(vertex) {
minx = Math.min(minx, vertex.x);
miny = Math.min(minx, vertex.y);
maxx = Math.max(maxx, vertex.x);
maxy = Math.max(maxx, vertex.y);
});
var dx = (maxx - minx) * 10,
dy = (maxy - miny) * 10;
var v0 = new Vertex(minx - dx, miny - dy * 3),
v1 = new Vertex(minx - dx, maxy + dy),
v2 = new Vertex(maxx + dx * 3, maxy + dy);
return new Triangle(v0, v1, v2);
};
An alternative method which is maybe a bit more elegant, and maybe not as complicated as finding the minimum bounding triangle, is by finding the Minimum Enclosing Circle first, with Welzl's algorithm that conveniently runs in O(n) time, and then spanning a triangle around this enclosing circle. A javascript implementation of a minimum enclosing circle algo can be found here by Project Nayuki. Then the enclosing triangle would simply be one that is spanned on a circle with twice the diameter of the minimum enclosing circle.
Triangulation Procedure
Here's an example of how the algorithm works on a larger set of points (rerun a it a couple of times to see the procedure):
With all of the previous parts in place, the remainder of the triangulation procedure becomes very straightforward! In this section we will iteratively add the triangulation vertices to the triangulation mesh and resolve the areas of conflict where vertices fall into the circumcircle of other triangles. This is done by removing the conflicting triangles, in turn creating a polygonal hole that can be patched up with a set of new triangles, by connecting the vacant edges with the current vertex in question. Doing this exactly as described by the pseudocode snippet may end up being a very inefficient way to do it, rather than comparing every triangle's edges against every other triangle's edges, we may actually just compare all edges and store the ones that are unique in a separate array to construct the polygonal hole.
With these considerations, we can model our procedure as follows:
function triangulate(vertices) {
// Create bounding 'super' triangle
var st = makeSuperTriangle(getEnclosingCircle(pointList));
// Initialize triangles while adding bounding triangle
var triangles = [st];
// Triangulate each vertex
vertices.forEach(function(vertex) {
triangles = addVertex(vertex, triangles);
});
// Remove triangles that share edges with super triangle
triangles = triangles.filter(function(triangle) {
return !(triangle.v0 == st.v0 || triangle.v0 == st.v1 || triangle.v0 == st.v2 ||
triangle.v1 == st.v0 || triangle.v1 == st.v1 || triangle.v1 == st.v2 ||
triangle.v2 == st.v0 || triangle.v2 == st.v1 || triangle.v2 == st.v2);
});
return triangles;
};
Essentially we first create the super triangle as discussed earlier, and add it to the triangulation to get things rolling initially. Then we add one vertex at a time and do the bulk of the procedure in the addVertex() function. As a final step we also need to remove all triangles that share an edge with the original super triangle, since it was never part of the triangulation. As for the addVertex() function:
// Update array of triangles by adding a new vertex
var addVertex = function(vertex, triangles) {
var edges = [];
// Remove triangles with circumcircles containing the vertex
triangles = triangles.filter(function(triangle) {
if (triangle.inCircumcircle(vertex)) {
edges.push(new Edge(triangle.v0, triangle.v1));
edges.push(new Edge(triangle.v1, triangle.v2));
edges.push(new Edge(triangle.v2, triangle.v0));
return false;
}
return true;
});
// Get unique edges
edges = uniqueEdges(edges);
// Create new triangles from the unique edges and new vertex
edges.forEach(function(edge) {
triangles.push(new Triangle(edge.v0, edge.v1, vertex));
});
return triangles;
};
Here we can conveniently make use of the filter() function that is applicable to arrays in javascript. The filter function creates a new array from all the elements that pass the condition that it's called upon. In this case the condition is actually another function that checks if the vertex falls into the circumcircle of the triangle, if it does we take the edges of this triangle and store them in the edges array, we'll need them in a second. If the vertex is not in the circumcircle, we can just ignore it as it is a valid triangle. Having obtained the edges, we now need to check which ones are unique, remember, as explained earlier, the edges that are not shared are those that fall onto the boundary of the polygonal hole. We do it in this manner, with the uniqueEdges() function:
// Remove duplicate edges
var uniqueEdges = function(edges) {
var uniqueEdges = [];
for (var i = 0; i < edges.length; ++i) {
var isUnique = true;
// See if edge is unique
for (var j = 0; j < edges.length; ++j) {
if (i != j && edges[i].equals(edges[j])) {
isUnique = false;
break;
}
}
// Edge is unique, add to unique edges array
isUnique && uniqueEdges.push(edges[i]);
}
return uniqueEdges;
};
With a nested for loop we determine for each edge wether it is unique or not. In the outer loop we set a flag for the current edge, assuming that it is unique. During the nested loop where we make another pass over the array where we compare that edge to all other edges (except at the same loop index), if we find a duplicate we set the flag to false. Once this inner loop completes, we check the flag, and only in the case of it being unique we store in an array uniqueEdges which will be returned to the addVertex() function. Those unique edges then make up the boundary of the polygonal hole that needs to be re-triangulated. This iterative procedure thus eliminates all invalid triangles and re-triangulates them into smaller ones until we obtain a valid Delaunay Mesh!
Putting it all together!
And finally let's put everything together! The final code ends up being relatively long, so here's a working example using p5js (I've included everything required like the circumcircle computation as well):
Using the Delaunator Class
And lastly, I want to include a section on using the delaunator, because in most projects it's probably better to use an efficient library rather than reinventing the wheel. You can find the library here, where you're provided with a couple of options to integrate it with your project depending on your preferences and needs. I like to simply include it like this:
<script src="https://unpkg.com/delaunator@5.0.0/delaunator.min.js"></script>
Then we need to create the initialize the Delaunator on a list of coordinates. Note that these coordinates should be in form of a flat list:
// coordinate list of the Delaunay vertices
const coords = [168,180, 168,178, 168,179, 168,181, 168,183, ...];
const delaunay = new Delaunator(coords);
console.log(delaunay.triangles);
// [623, 636, 619, 636, 444, 619, ...]
You can then get information about the triangles in the following manner:
// coordinate list of the Delaunay vertices
const coords = [168,180, 168,178, 168,179, 168,181, 168,183, ...];
const delaunay = new Delaunator(coords);
let triangles = delaunay.triangles
for (let i = 0; i < triangles.length; i += 3) {
coordinates.push([
points[triangles[i]],
points[triangles[i + 1]],
points[triangles[i + 2]]
]);
}
And I think you get the idea. There's a lot more things you can do with the Delaunator library, go check out the github repo.
And that's a wrap! If you've reached here, thanks a million for reading! If you enjoyed this tutorial consider sharing it with your friends, it helps out quite a bit. Cheers!
If you enjoyed this post, you might also like: