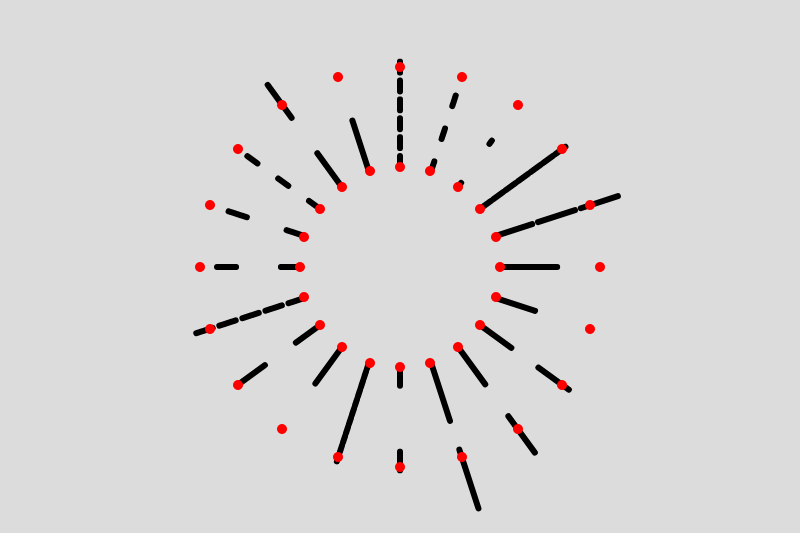
Okay, so this is a long one. Drawing dashed lines in P5 from scratch and animating them was a tough one, but I'm super happy with my results and stoked to share the code in this post, especially with the insights I've gained from writing this code. I highly recommend attempting to make what you see above from scratch on your own, and then come back when you hit a roadblock, otherwise enjoy the post! Let's go:
- Dashed lines with the js drawing context
- Drawing a line between two coordinates
- Adding the dashed line style
- Fixing the final protruding dash
- Code for static dashed lines
- Pumping forward animation
- Cleaning up the animation
- Final code for animation
- Reverse Speed
Dashed lines with the drawing Context
Drawing a line in P5JS is very easy and can be done with a single line of code. You simply need to know the coordinates of the starting point and the end point:
line(0,0,100,100)
Drawing a dashed line in P5JS is also relatively easy, however requires you to invoke the 'drawingContext' as pointed out in this Github issue:
drawingContext.setLineDash([5, 15]);
line(0,0,100,100)
The setLineDash() function receives an array of two parameters which specify the length of the dashes that will make up your line and the spacing in between these dashes. If you simply want to draw dashed or dotted lines this might be sufficient for you. However I wanted a little more comlpex behaviour from my lines.
Drawing a line between two Points
Drawing custom dashed lines from scratch, that have an animated behaviour, requires quite a little bit of code. What follows is my attempt at making animated dashed lines in P5JS, but is no way the optimal approach to doing so.
As usual, we will heavily rely on Object Oriented programming by modeling the dashed line as a class and giving it behaviour through functions and member variables. First order of business will be drawing a line manually between two sets of coordinates. This involves finding the angle that the line forms with the x axis, which can be done with the atan2() function:
// angle formed by the line going from point (x1,y1) to point (x2,y2)
// and the positive x-axis at the coordinate origin
slope = atan2(y2 - y1, x2 - x1)
The atan2() function is super useful in many scenarios as it gives you the angle formed by a line and the x-axis, here we use it to find the angle of the line which we require to correctly slant the line that we will draw. Additionally, we will also require the length of the segment between the two points, the formula for that is:
// length of line going from point (x1, y1) to point (x2, y2)
L = sqrt(pow((x1 - x2), 2) + pow((y1 - y2), 2));
The result given by atan2 defines the angle of inclination of our line, which we will rotate by that angle. Essentially, we will center a circle on the point (x1, y1) with a radius equal to the length of the line (which we just calculated) and use the angle with sin() and cos() to slant the line. If you haven't already done so, go and read my post that explains rotation in detail here.
So far our class will look like this:
class SlopeLine {
constructor(x1, y1, x2, y2, segmentLength, spaceLength) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.segmentLength = segmentLength;
this.spaceLength = spaceLength;
this.L = sqrt(
pow((this.x1 - this.x2), 2) +
pow((this.y1 - this.y2), 2));
this.S = atan2(this.y2 - this.y1, this.x2 - this.x1)
}
display() {
line(this.x1, this.y1,
this.x1 + this.L * cos(this.S),
this.y1 + this.L * sin(this.S))
}
}
function setup() {
createCanvas(400, 400);
sl = new SlopeLine(200, 200, 300, 200);
}
function draw() {
background(220);
sl.display();
}
Not very impressive yet, because it's essentially just doing the same thing that you could do with the line() function. Nonetheless, it involves some very important calculations that are useful for many scenarios.
Dashed line style
Now we'll tackle the main problem, achieving the dashed line style. Similarly to invoking the drawingContext, we want to be able to freely set the dash length as well as the length of the gaps between dashes. We've already calculated the length of our line, next we'll have to calculate how many segments we can fit into it:
numSegments = L / (segmentLength + spacing);
We simply divide the overall length of the line by the combined length of a dash and a gap. This calculation will not always give us a round number, and at this point we encounter our first problem, how do we split up a segment of fixed length into a number of sub-segments, whose combined length might not exactly add up to the total length of the entire segment?
In actuality, we have to consider two cases, the segment and space length either add up exactly n times to fill out the segment, or they don't. If they do add up, great! Otherwise, we'll have to write some code to handle that case.
Let's first have a look at what it looks like without handling that case:
class SlopeLine {
constructor(x1, y1, x2, y2, segmentLength, spaceLength) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.segmentLength = segmentLength;
this.spaceLength = spaceLength;
// Calculate length
this.L = sqrt(
pow((this.x1 - this.x2), 2) +
pow((this.y1 - this.y2), 2));
// calculate angle
this.S = atan2(this.y2 - this.y1, this.x2 - this.x1)
// calculate number of segments
this.numS = this.L / (this.segmentLength+this.spaceLength)
console.log(this.numS)
}
display() {
for(let i = 0; i < this.numS; i++){
console.log(i)
line(
this.x1 + (this.segmentLength + this.spaceLength)*i*cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength)*i*sin(this.S),
this.x1 + (this.segmentLength+ this.spaceLength)*(i+1)*cos(this.S)-this.spaceLength*cos(this.S),
this.y1 + (this.segmentLength+ this.spaceLength)*(i+1)*sin(this.S)-this.spaceLength*sin(this.S),
)
}
}
}
function setup() {
createCanvas(400, 400);
sls = [];
for(i = 0; i < 20; i++){
sls.push(new SlopeLine(100, 100+10*i, 300, 100+10*i, random(1,35),random(1,35)));
}
}
function draw() {
background(220);
for(i = 0; i < 20; i++){
stroke(0)
strokeWeight(3);
sls[i].display();
// Additionally we're gonna draw two red points to see where the line should start and end
strokeWeight(5);
stroke(255,0,0)
point(100,100+i*10);
point(300,100+i*10);
}
}

Here we're actually drawing a couple of lines with the dash length and in-between spacing randomized. The red points show where the line starts and where it should end. You can see that in some cases the last dash protrudes further than the second red dot. My OCD thinks that this looks very bad and that this needs to be fixed. Let's also see what it looks like if we spread these lines on an arc or around a circle:
function setup() {
createCanvas(400, 400);
sls = [];
radius = 50;
for(i = 0; i < 20; i++){
sls.push(new SlopeLine(200+radius*cos(TWO_PI/20*i),
200+radius*sin(TWO_PI/20*i),
200+radius*cos(TWO_PI/20*i)*2,
200+radius*sin(TWO_PI/20*i)*2,
random(1,35),
random(1,35)));
}
}
function draw() {
background(220);
for(i = 0; i < 20; i++){
stroke(0)
strokeWeight(3);
sls[i].display();
// Additionally we're gonna draw two red points to see where the line should start and end
strokeWeight(5);
stroke(255,0,0)
point(200+radius*cos(TWO_PI/20*i),
200+radius*sin(TWO_PI/20*i));
point(200+radius*cos(TWO_PI/20*i)*2,
200+radius*sin(TWO_PI/20*i)*2);
}
}

Fixing the final protruding Dash
This was genuinely... chllenging, to fix. A first thought was to simply check if the length of n * (segment length + space length) exceeds the length of the segment, and then discard the last dash. But that turned out to be quite ugly as well, as you can see here:

We'll have to make a check just for the last dash, this can be done by finding the total length of all segments and spaces:
var check = sqrt(
pow((this.segmentLength + this.spaceLength)*(int(this.numS)+1)*sin(this.S)-this.spaceLength*sin(this.S), 2 )
+ pow((this.segmentLength + this.spaceLength)*(int(this.numS)+1)*cos(this.S)-this.spaceLength*cos(this.S), 2)
)
Notice that we're casting 'this.numS' to an integer, this was maybe the one thing that I was stuck on for a while. We're casting to an integer to be able to draw an exact number of segments and spaces. We're also adding 1 to the number of segments because we're stopping the previous for loop at 'this.numS-1'. Then we also subtract one length of a spacing, since we only care about where the dash ends, not where the dash and it's following space end. If we now draw a green point at this position, we obtain:
stroke(0,255,0)
strokeWeight(5)
point(this.x1 +
(this.segmentLength+ this.spaceLength)*
(int(this.numS)+1)*cos(this.S)-
this.spaceLength*cos(this.S),
this.y1+(this.segmentLength + this.spaceLength)*
(int(this.numS)+1)*sin(this.S)-
this.spaceLength*sin(this.S)
)

Next we just need to check if the length of the last dash exceeds the total length of the line or not, and draw the lines accordingly:
stroke(255,255,0)
strokeWeight(3)
if(checkthis.L){
line(
this.x1 + (this.segmentLength + this.spaceLength)*(int(this.numS))*cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength)*(int(this.numS))*sin(this.S),
this.x2,
this.y2
)
}
Here you can see in yellow the final dash segments and the green point indicates where the segment would have ended otherwise. Is this the best solution? I don't know, but it works:

Drawing dashed lines
If we combine everything we have so far, our class will look like this:
class DashLine {
constructor(x1, y1, x2, y2, segmentLength, spaceLength) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.segmentLength = segmentLength;
this.spaceLength = spaceLength;
// Calculate length
this.L = sqrt(
pow((this.x1 - this.x2), 2) +
pow((this.y1 - this.y2), 2));
console.log(this.L)
// calculate angle
this.S = atan2(this.y2 - this.y1, this.x2 - this.x1)
// calculate number of segments
this.numS = this.L / (this.segmentLength+this.spaceLength)
console.log(this.numS)
// calculate length of tail
this.tailL = this.L % (this.segmentLength+this.spaceLength)
}
display() {
for(let i = 0; i < this.numS-1; i++){
//console.log(i)
line(
this.x1 + (this.segmentLength + this.spaceLength)icos(this.S),
this.y1 + (this.segmentLength + this.spaceLength)isin(this.S),
this.x1 + (this.segmentLength+ this.spaceLength)(i+1)cos(this.S)-this.spaceLengthcos(this.S),
this.y1 + (this.segmentLength+ this.spaceLength)(i+1)sin(this.S)-this.spaceLengthsin(this.S)
)
}
var check = sqrt(
pow((this.segmentLength + this.spaceLength)*(int(this.numS)+1)*sin(this.S)-this.spaceLength*sin(this.S), 2 )
+ pow((this.segmentLength + this.spaceLength)*(int(this.numS)+1)*cos(this.S)-this.spaceLength*cos(this.S),2)
)
stroke(0,255,0)
strokeWeight(5)
point(this.x1 +
(this.segmentLength+ this.spaceLength)*
(int(this.numS)+1)*cos(this.S)-
this.spaceLength*cos(this.S),
this.y1+(this.segmentLength + this.spaceLength)*
(int(this.numS)+1)*sin(this.S)-
this.spaceLength*sin(this.S)
)
stroke(255,255,0)
strokeWeight(3)
if(check<this.L){
line(
this.x1 + (this.segmentLength + this.spaceLength)*(int(this.numS))*cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength)*(int(this.numS))*sin(this.S),
this.x1 + (this.segmentLength+ this.spaceLength)*((int(this.numS))+1)*cos(this.S)-this.spaceLength*cos(this.S),
this.y1 + (this.segmentLength+ this.spaceLength)*((int(this.numS))+1)*sin(this.S)-this.spaceLength*sin(this.S)
)
}else if(check>=this.L){
line(
this.x1 + (this.segmentLength + this.spaceLength)*(int(this.numS))*cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength)*(int(this.numS))*sin(this.S),
this.x2,
this.y2
)
}
}
}
function setup() {
createCanvas(400, 400);
dls = [];
for(i = 0; i < 20; i++){
dls.push(new DashLine(100, 100+10i, 300, 100+10i, random(1,35),random(1,35)));
}
}
function draw() {
background(220);
for(i = 0; i < 20; i++){
stroke(0)
strokeWeight(3);
dls[i].display();
// Additionally we're gonna draw two red points to see where the line should start and end
strokeWeight(5);
stroke(255,0,0)
point(100,100+i*10);
point(300,100+i*10);
This works, and it even works for any numbers that you give as parameters for segment length and spacing length. Except for negative numbers, which don't make sense to begin with and can be checked for in the constructor.
Forward Motion

Next we'll want to look into conveying motion with the dashes, which is a little tricky but actually easier than you might think. We want them to flow from the start of the line towards the end, where they seemingly disappear and reappear at the beginning of the line. Since we already wrote solid code, it won't take many modifications to achieve this effect. First, we'll have to create a parameter called 'this.beginningLength', which stores the amount of displacement from the intial point. The class now becomes:
class AnimatedLine {
constructor(x1, y1, x2, y2, segmentLength, spaceLength) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.segmentLength = segmentLength;
this.spaceLength = spaceLength;
// Calculate length
this.L = sqrt(
pow((this.x1 - this.x2), 2) +
pow((this.y1 - this.y2), 2));
console.log(this.L)
// Calculate angle
this.S = atan2(this.y2 - this.y1, this.x2 - this.x1)
// Calculate number of segments
this.numS = this.L / (this.segmentLength+this.spaceLength)
console.log(this.numS)
this.beginningLength = 0;
}
move(rate){
this.beginningLength += rate
if(this.beginningLength>this.segmentLength+this.spaceLength){
this.beginningLength = 0;
}
}
display() {
for(let i = 0; i < this.numS; i++){
line(
this.x1 + (this.segmentLength + this.spaceLength)*i*cos(this.S)
+ this.beginningLength*cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength)*i*sin(this.S)
+ this.beginningLength*sin(this.S),
this.x1 + (this.segmentLength+ this.spaceLength)*(i+1)*cos(this.S)
-this.spaceLength*cos(this.S) + this.beginningLength*cos(this.S),
this.y1 + (this.segmentLength+ this.spaceLength)*(i+1)*sin(this.S)
-this.spaceLength*sin(this.S) + this.beginningLength*sin(this.S)
)
}
var check = sqrt(
pow((this.segmentLength + this.spaceLength)*(int(this.numS)+1)*sin(this.S)
-this.spaceLength*sin(this.S)+ this.beginningLength*sin(this.S), 2)
+ pow((this.segmentLength + this.spaceLength)*(int(this.numS)+1)*cos(this.S)
+ -this.spaceLength*cos(this.S)+ this.beginningLength*cos(this.S), 2)
)
}
}
function setup() {
createCanvas(400, 400);
als = [];
for(i = 0; i < 20; i++){
als.push(new AnimatedLine(100, 100+10*i, 300, 100+10*i, random(1,35),random(1,35)));
}
}
function draw() {
background(220);
for(i = 0; i < 20; i++){
stroke(0)
strokeWeight(3);
als[i].display();
als[i].move(0.2)
// Additionally we're gonna draw two red points to see where the line should start and end
strokeWeight(5);
stroke(255,0,0)
point(100,100+i*10);
point(300,100+i*10);
}
}
And we end up with something similar to this:

The most important new addition is the move() function, which displaces the beginningLength parameter, which is what's pushing forward the dashed line. Once the beginningLength parameter is larger or equal to the length of a dash and a gap we reset it. The beginningLength parameter will be included in the calculation of the position of each dash.
Watching this go on for a little while, you can see how unsatisfying it is to see the first dash of each line pop up out of seemingly nowhere, and equivalently we again have a problem of a protruding final dash.
Cleaning up the Animation
We need to draw the line that goes from the first red point to the beginning of the space preceding the first dash. This simulates as if the dashed line is continuously appearing from the left side, and already makes the animation look much less jumpy:
// Add this to beginning of display function
if(this.beginningLength > this.spaceLength){
stroke(255,0,255)
line(this.x1, this.y1,
this.x1 + (this.beginningLength-this.spaceLength)*cos(this.S),
this.y1+ (this.beginningLength-this.spaceLength)*sin(this.S)
)
}
Now we have something that looks like this:
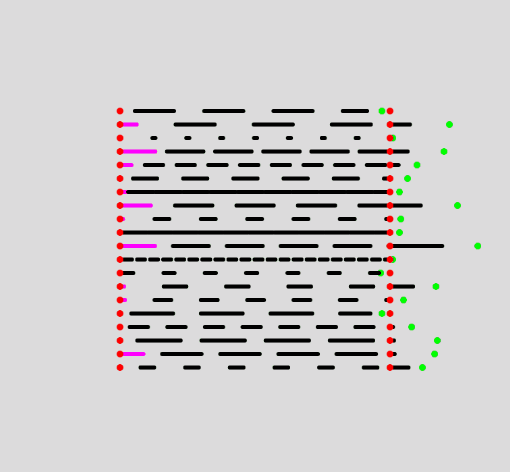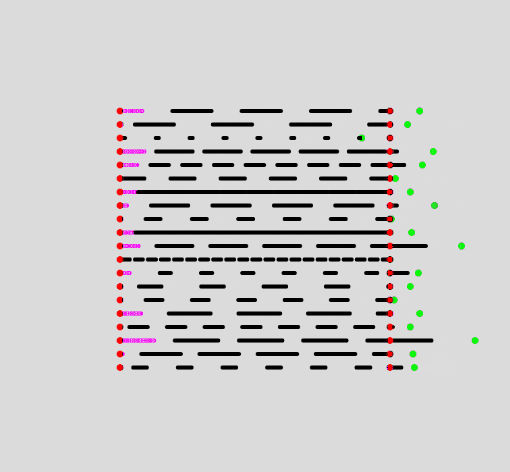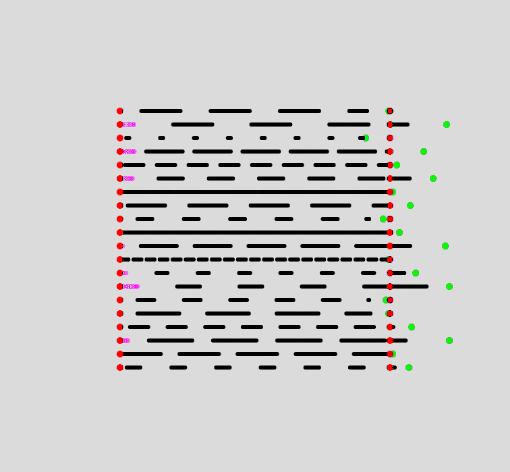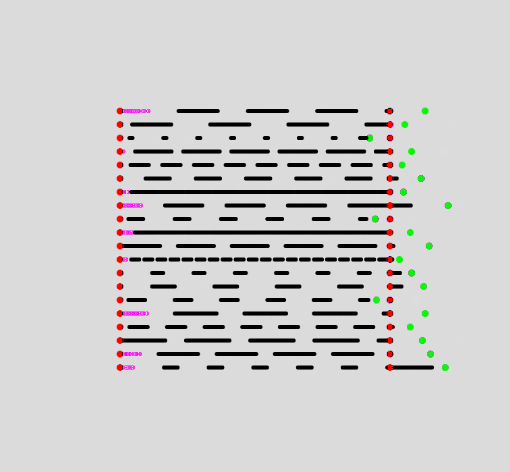
Now to the truncation of the newly protruding last dash. One step towards a solution will be checking if any of the drawn dashes exceed the total length of our line, if they do, we simply don't draw them:
class AnimatedLine {
constructor(x1, y1, x2, y2, segmentLength, spaceLength) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.segmentLength = segmentLength;
this.spaceLength = spaceLength;
// Calculate length
this.L = sqrt(
pow((this.x1 - this.x2), 2) +
pow((this.y1 - this.y2), 2));
console.log(this.L)
// calculate angle
this.S = atan2(this.y2 - this.y1, this.x2 - this.x1)
// calculate number of segments
this.numS = this.L / (this.segmentLength + this.spaceLength)
// calculate length of tail
this.tailL = this.L % (this.segmentLength + this.spaceLength)
this.beginningLength = 0;
this.tailLength = this.tailL;
this.difference = (this.segmentLength + this.spaceLength)
}
move(rate) {
this.beginningLength += rate
if (this.beginningLength >= this.segmentLength + this.spaceLength) {
this.beginningLength = 0;
}
this.difference = (this.segmentLength + this.spaceLength)-this.beginningLength
}
display() {
if (this.beginningLength > this.spaceLength) {
stroke(255, 0, 255)
line(this.x1, this.y1,
this.x1 + (this.beginningLength - this.spaceLength) * cos(this.S),
this.y1 + (this.beginningLength - this.spaceLength) * sin(this.S))
}
stroke(0)
for (let i = 0; i < this.numS; i++) {
// check if dash segment exceeds total line length
var distCheck = sqrt(
pow((this.segmentLength + this.spaceLength) * (i + 1)
* cos(this.S) - this.spaceLength * cos(this.S)
+ this.beginningLength * cos(this.S), 2)
+ pow((this.segmentLength + this.spaceLength) * (i + 1)
* sin(this.S) - this.spaceLength * sin(this.S)
+ this.beginningLength * sin(this.S), 2)
)
// if it does, we simply don't draw it
if (distCheck <= this.L) {
line(
this.x1 + (this.segmentLength + this.spaceLength) * i
* cos(this.S) + this.beginningLength * cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength) * i
* sin(this.S) + this.beginningLength * sin(this.S),
this.x1 + (this.segmentLength + this.spaceLength) * (i + 1)
* cos(this.S) - this.spaceLength * cos(this.S)
+ this.beginningLength * cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength) * (i + 1)
* sin(this.S) - this.spaceLength * sin(this.S)
+ this.beginningLength * sin(this.S)
)
}
}
}
}
function setup() {
createCanvas(400, 400);
als = [];
for (i = 0; i < 20; i++) {
als.push(new AnimatedLine(100, 100 + 10 * i, 300, 100 + 10 * i, random(1, 35), random(1, 35)));
}
}
function draw() {
background(220);
for (i = 0; i < 20; i++) {
stroke(0)
strokeWeight(3);
als[i].display();
als[i].move(0.2)
strokeWeight(5);
stroke(255, 0, 0)
point(100, 100 + i * 10);
point(300, 100 + i * 10);
}
}
And we end up with this:

Now the protruding dash doesn't appear anymorer but we have a weird behaviour where the last dash simply disappears. We don't want that, we can fix it with an additional check and mirroring the beginningLength dash, since their lengths are proportional.
Final Code
And the final code goes here:
class AnimatedLine {
constructor(x1, y1, x2, y2, segmentLength, spaceLength) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
this.segmentLength = segmentLength;
this.spaceLength = spaceLength;
// Calculate length
this.L = sqrt(
pow((this.x1 - this.x2), 2) +
pow((this.y1 - this.y2), 2));
console.log(this.L)
// calculate angle
this.S = atan2(this.y2 - this.y1, this.x2 - this.x1)
// calculate number of segments
this.numS = this.L / (this.segmentLength + this.spaceLength)
this.beginningLength = 0;
}
move(rate) {
this.beginningLength += rate
if (this.beginningLength >= this.segmentLength + this.spaceLength) {
this.beginningLength = 0;
}
}
display() {
if (this.beginningLength > this.spaceLength) {
stroke(255, 0, 255)
line(this.x1,
this.y1,
this.x1 + (this.beginningLength - this.spaceLength) * cos(this.S),
this.y1 + (this.beginningLength - this.spaceLength) * sin(this.S)
)
}
for (let i = 0; i < this.numS; i++) {
stroke(0)
var distCheck = sqrt(
pow(
(this.segmentLength + this.spaceLength) * (i + 1)
* cos(this.S) - this.spaceLength * cos(this.S)
+ this.beginningLength * cos(this.S), 2)
+ pow((this.segmentLength + this.spaceLength) * (i + 1)
* sin(this.S) - this.spaceLength * sin(this.S)
+ this.beginningLength * sin(this.S), 2))
if (distCheck <= this.L) {
line(
this.x1 + (this.segmentLength + this.spaceLength) * i
* cos(this.S) + this.beginningLength * cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength) * i
* sin(this.S) + this.beginningLength * sin(this.S),
this.x1 + (this.segmentLength + this.spaceLength) * (i + 1)
* cos(this.S) - this.spaceLength * cos(this.S)
+ this.beginningLength * cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength) * (i + 1)
* sin(this.S) - this.spaceLength * sin(this.S)
+ this.beginningLength * sin(this.S)
)
} else {
stroke(255,255,0)
var distCheck =
sqrt(
pow((this.segmentLength + this.spaceLength) * i
* cos(this.S) + this.beginningLength * cos(this.S), 2)
+ pow((this.segmentLength + this.spaceLength) * i
* sin(this.S) + this.beginningLength * sin(this.S), 2))
if (distCheck < this.L) {
line(
this.x1 + (this.segmentLength + this.spaceLength) * i
* cos(this.S) + this.beginningLength * cos(this.S),
this.y1 + (this.segmentLength + this.spaceLength) * i
* sin(this.S) + this.beginningLength * sin(this.S),
this.x2, this.y2
)
}
}
}
}
}
function setup() {
createCanvas(400, 400);
als = [];
for (i = 0; i < 20; i++) {
als.push(new AnimatedLine(100, 100 + 10 * i, 300, 100 + 10 * i, random(1, 35), random(1, 35)));
}
}
function draw() {
background(220);
for (i = 0; i < 20; i++) {
stroke(0)
strokeWeight(3);
als[i].display();
als[i].move(0.2)
strokeWeight(5);
stroke(255, 0, 0)
point(100, 100 + i * 10);
point(300, 100 + i * 10);
}
}
As sanity check, it works fine with any kind of slanted lines as well:
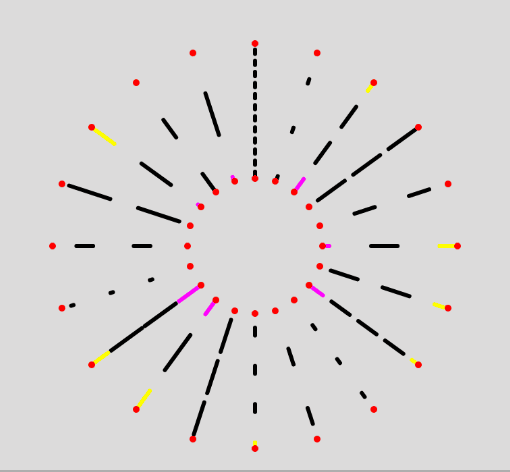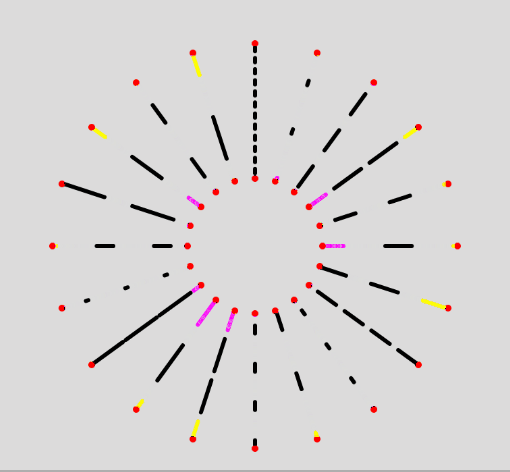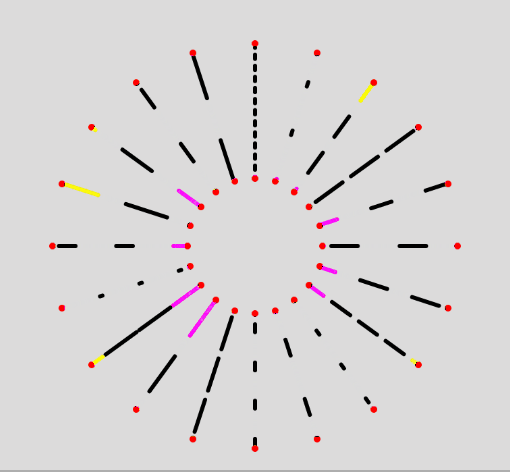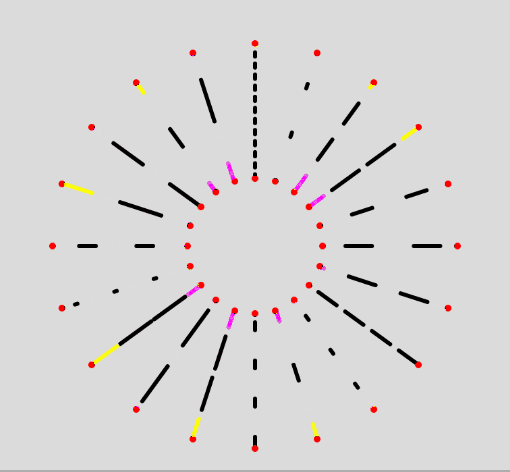
Reverse Movement
One final addendum would be reversing the movement to go in the other direction. Sometimes I surprise myself with the code I write, what we have was solid enough that a simple change was all we needed to handle the reverse movement. We simply add a function that handles negative rates passed to the move function. In this case the beginningLength begins from (segmentLength + spaceLength) and decreases gradually, and is reset when it becomes 0. The code looks like this:
move(rate) {
if(rate= this.segmentLength + this.spaceLength) {
this.beginningLength = 0;
}
}
}
moveReverse(rate) {
this.beginningLength += rate
if (this.beginningLength <= 0) {
this.beginningLength = this.segmentLength + this.spaceLength;
}
}
And this should be a wrap. Now you can go ahead and use these dashed lines for your own sketches or build upon them! Happy creative coding!